三、标准分的实际意义

有甲乙两个班级，现有两名学生A和B，分别来自甲、乙两班。如果他们的考试分数相同，那么能说这两名学生在班上的成绩一样吗？

关注点：两个班级的成绩均值、标准差

存在三种情形：

（1）均值相同，标准差不一样；

（2）均值不同，标准差一样；

（3）均值与标准差，都不一样；

可以用标准分对不同总体进行合理的比较

例题1：A与B两人都考了80分，甲班均值80分，乙班均值60分，标准差都是10分。试比较A、B两学生在班级里的成绩。

Z(A)=(80分-80分)/10分=0     Z(B)=(80分-60分)/10分=2 Z(B)>Z(A)

例题2：A与B两人都考了80分，甲乙两班均值都是60分，甲班标准差是10分，乙班标准差是20分。试比较A、B两学生在班级里的成绩。

Z(A)=(80分-60分)/10分=2     Z(B)=(80分-60分)/20分=1  Z(A)> Z(B)

除了用于不同总体间取值进行比较外，还用于不同总体间综合指标的比较，如城市之间总体发展指数比较：

城市发展有关指标：

1.工业企业数量；       5.社会零售商品总产值；

2.轻工业总产值；       6.零售点总数；

3.重工业总产值；       7.服务点总数；

4.科技人员总数；       8.工资总额；

每个城市的总得分为：

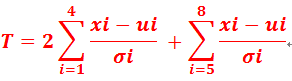
注：上述公式内“2”表示前四项的权重更大

第三节 标准正态分布表的使用

F(Z)为标准正态分布从-   到Z的分布面积

Z=0时，F(Z)=0.5；Z=1时，F(Z)=0.8413；

任意两点[Z1、Z2]之间的面积为F(Z2)的面积减去F(Z1)的面积；

当Z为无限大时，F( )=1

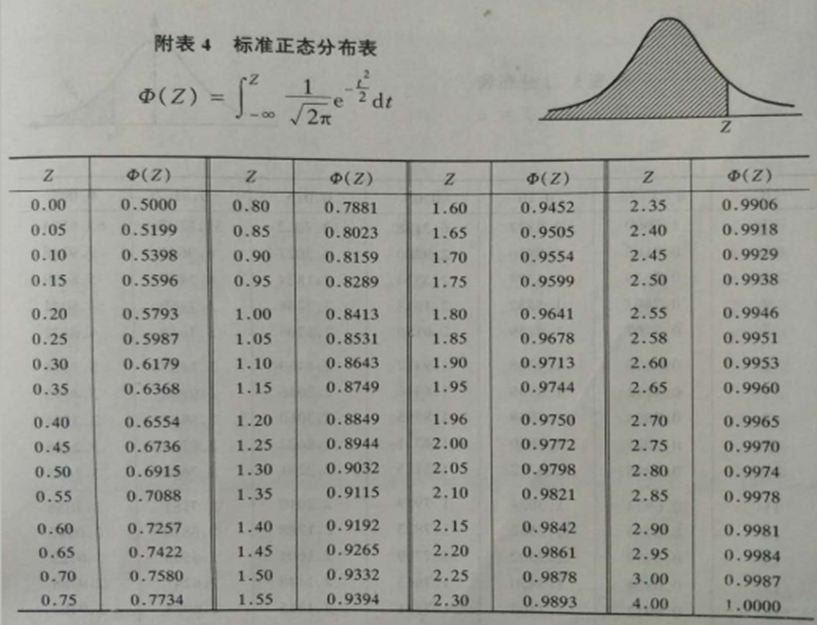
例题：已知ε服从标准正态分布N（0，1），求P（ε≤1.3）=？

P(ε≥1.3)=?  P(ε≤-1.3)=?  P(1.3≤ε≤2.3)=?

标准正态分布，P(ε≤1.3)=φ(1.3)=0.9032

               P(ε≥1.3)=1-φ(1.3)=0.0968

               P(ε≤-1.3)= 1-φ(1.3)=0.0968

               P(1.3≤ε≤2.3)=φ(2.3)-φ(1.3)=0.0861

根据视频授课内容，进行随堂练习，将结果反馈在QQ群内。

如果ε服从标准正态分布N（0，1），

求P(-2.3≤ε≤-1.3)=？ 求P(|ε|≥λ)=0.05中的λ值

例题：北京市初婚年龄服从正态分布，其均值为25岁，标准差为5岁，问25岁到30岁之间结婚的人，其百分数是多少？

将年龄转化成标准分，Z1=(25岁-25岁)/5岁=0    Z2=(30岁-25岁)/5岁=1

φ(Z2)-φ(Z1)=0.8413-0.5=0.3413

25岁到30岁结婚的人，比例约为34.13%