▇ 相对坐标系与绝对坐标系的采用及其转换问题 

   在研究和解决叶轮机实际流动问题时，必须选择合适的坐标体系，建立和采用相配套的力学模型和分析方法！ 

   对于与固体动轮固连在一起的建模参照坐标系，我们常简称为“相对坐标系”。站在相对坐标系上的假想观察者，称为相对观测者，其所观测到的流动参数即为“相对流动和相对流动参数”。当相对坐标系为非惯性系时，不能直接应用宏观经典的牛顿第二定理公式。

   比如，如果所选取的建模参照坐标系与固体机体或大地等是固连在一起的，并假想观测者站在其上，则此观测者就称为绝对观测者，其所观测到的流动参数即为“绝对流动和绝对流动参数”，此坐标系就称之为“绝对坐标系”。当绝对坐标系为惯性坐标体系时，可以直接应用牛顿第二定律等公式。      

  这两种坐标系各有其优点。比如，谈静轮内工质介质的运动，流动的相对运动与绝对运动是一致的；对于动轮内工质的运动建模和研究，既可采用相对座标系，也可采用绝对坐标系，这要根据实际情况和你的目的需要来确定。

   总之，在旋转叶轮机械气体动力学问题的研究和解决中，坐标体系的转换是经常性的或随时随地的活动！无论是相对坐标系，还是绝对座标系，都具有重要的地位所在，二者相辅相成、互为补充！

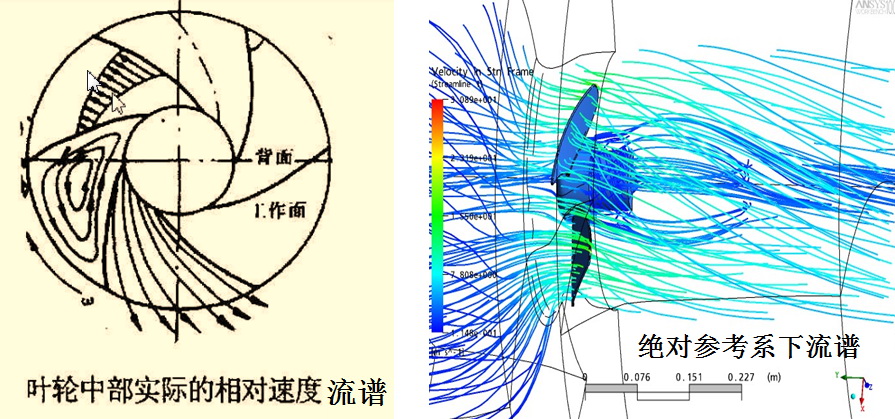
  无论是绝对观测者，还是相对观测者，所观测到的都是同一个客观存在着的客观流场！基于此根本点，以牵连运动为中介，就能够建立两种流动运动参数之间的内在关联关系！

▇ 气流静参数和总参数与坐标系关系

   气体的热力学状态点参数（为标量有值无方向限制，包括内能，温度、密度、压强，焓，熵），不论气体系统是运动的或静止的，都是其自身随体或附体存在的客观物理属性（缘于气体分子无规则不停歇的热运动），其大小均是不随建模参照座标系的变换而改变的，故也常称为静参数（随体参数），以区别于相应状态点处所对应的总参数！

   气流滞止或总参数，因其与流体气团的宏观运动速度或动能有关，故其值是与观测者所在位置不同或参照坐标系选择不同而紧密相关的！流场中，任意一点处总是同时存在两大套参数：一套是静参数（常表示为p，T等），至少一套的总参数（常表示为等）。

▇ 动坐标系下的叶片机一元气流能量方程

   ○可推出在与外界绝热时，在随叶轮一起旋转的动坐标系即相对坐标系下，控制体CV中一元稳定流动、热焓形式的能量方程式为：   

  ○那么在动坐标系下，相应沿一元流管CV的机械能形式的能量方程式即广义的伯努利方程式又该如何的表达？