第二章 航空叶片机气动热力学
基础知识回顾与补充
▇ 热力学可压缩气流概念和模型化
流动过程中与功、热相关联的能量项是焓,叶轮机内流的比焓。在叶轮机械的内部流动过程中,热损失较小,常假设其内流为绝热过程。如果不考虑流动过程的摩擦损失,则流动过程认为是等熵的,这是一种理想模化的模型。
通常在工程初步设计和分析上,叶轮机械的㊣内部流动(内流)可按可压缩等熵过程进行计算,然后再结合某种效率或损失项来进行一定修正处理。
本课程流速用符号c来表示,介质声速用符号a表示。在临界条件下,Mcr=1,此时对应的声速称为临界声速,用acr 表示。气流速度与临界声速之比称为速度系数(因数),常用λ表示。在滞止温度保持不变(定常稳态,与外界无热量和功交换)的流动变化过程中,临界声速值保持不变,但当地声速却随静温的变化而变化,故使用中采用速度系数比采用马赫数要计算方便。
▇ 流动的滞止参数与常用气动函数
如果按一定的过程将气流速度滞止到零,此时此零速度状态的气流参数即称为对应该气流的滞止参数。在叶轮机械中,焓和动能两项之和常出现在方程中,把它们看成一个单一的组合量来使用,是较为方便的。
在绝能流动的条件下,气体的焓是随气流速度C的减小而增大的。如果把气流的速度绝能地滞止到0,此时所对应的焓值称之为滞止焓(总焓)。对应于滞止焓的温度称为滞止温度(总 温),在完全气体和定比热容的情况下,它可理解为:静温为T、速度为C的可压缩气体流动被绝热滞止后,所达到的温度值。滞止压强(总压强)可看成:静压强为p、流速为c (合速度)的可压缩气流被等熵滞止后所得到的压强值,该变化过程是等熵的。
○上面定义的滞止熵的概念是普遍适用的,它除了能量平衡关系以外,不包含任何假设条件;
○滞止温度只在完全气体和定比热容条件下才是严格适用的;
○滞止压强除与滞止温度有关的假设外,还有一个从静压强到总压强的等熵滞止条件,即滞止的途径应是等熵的。
○如果气体的流动过程是定常的,且与外界无功和热量交流,则流动过程的滞止焓和滞止温度不变且也不要求过程为等熵。
气体动力学函数在叶轮机械的气体动力学计算中有着广泛的应用。通过气动力函数,可将气流静参数与总参数的比值用马赫数或速度系数的函数来表示。课程中常用到的气动函数有四个。
▇ 叶片机内部气体流动特性的基本控制方程
与一般的管道流动(管流)和外部流动(外流)相比,叶片机械内部气体的运动更为复杂。这是由于叶片机内部既有静止的叶片排,又有旋转运动的叶片排,其流道的形状比较复杂,而且有机械轴功率的输入(压气机)或输出(涡轮)。
○叶片机内部气体流动的特点
1)流动的三维不均匀性;
2)流体的可压缩性作用;
3)流体的粘性剪切作用;
4)流动的高度非定常性。
○ 附面层与主流的相互干扰
○ 气流有较大的转折,参数变化梯度大
○ 叶轮机械内部复杂流动一般近似可用的适度简化:
1)选择合适坐标系等可使流动定常或准定常化;
2)流动通常情况具有轴对称性(叶片多而薄);
3)粘性作用主要在壁面附近粘性边界层中(设计工况和偏离不远的非设计工况)。

按照这些要求来分析气流的运动,所导出的运动微分方程统称为N-S方程,虽然这一方程组在理论上具有非常大的价值,但是在叶轮机械的工程设计应用中,理论求解这种含粘性项和时间偏导数项的非线性偏微分方程组、用以表达通过叶片和内外壁面所形成的复杂通道中的流动变化特性,仍然是非常复杂的、至少当前一般问题也是不可能解析求解的。
大量实践表明,在工程方案总体初步设计与总体基本特性分析时,通常应用一元稳定流动的基本方程和设计原理,大多是能够满足实际基本需求并方便快捷易用的。
所以以下主要给出气体一元稳定流动的基本控制方程组,课程将以定常一维流动规律和平面流场分布特性为主,展开对轴流叶片机气动工作原理的分析讲解与讨论。
(1)质量连续方程(涉及流速和质量流量表达)
质量连续方程是质量守恒定律用于欧拉流场下运动流体时的相应表达式。在定常一元稳定流动中,流过任一截面的质量流量都相等。在叶片机中,广泛应用的连续方程是以气流的滞止参数和气体动力学函数来表示的。研究通过旋转叶片排的流动,相对坐标系的采用是必须的,其中这里用下标w以表示相对值。
在叶轮机械的实验数据处理中,往往取为质量流量为坐标变数来绘制特性变化曲线,这样通过相似理论和无量纲化,可以使某一给定的实验结果能够应用于总压和总温不同于原始实验条件的不同情况。
(2A)热焓形式的能量方程式(直接体现热焓和动能之关系)
能量方程是热力学第一定律用于流动的流体时所得到的数学表达式,表达了流场中或流动过程中能量成分的转换关系。在稳定的一元流动中,对单位质量的气体而言,外界对气体所做的机械功加上气体与外界的热量交换,等于单位质量气体的焓增和动能、位能变化之和。由于没有涉及控制体内流动过程的具体情况,因此无论对可逆过程或不可逆过程,无论有无摩擦损失,方程都是适用的,对其的限制条件仅是流动一维的并定常。
(2B)机械能形式的能量方程式(伯努利方程式,直接体现流动的压能和动能之间的关系)
从热焓形式的能方程及热力学第一定律方程,可以推导获得运动流体一元流动模式下机械能形式的能量方程关系式,表达了气流产生或具有的压能(压力功)和宏观流速动能之间的定量转换关系。
○压气机段:在压气机段控制体内,积分形式压力功(积分静压能)称压气机多变压缩压力功(流动推进功)。
○涡轮机段:对于涡轮机段控制体内,积分形式压力功称多变膨胀功。
(3)动量(矩)守恒方程(体现流动的受力与动量的关系)
动量守恒方程是把经典牛顿第二定律转换应用到欧拉框架流场中运动流体所得到的相应数学控制表达式。分析流体与物体之间的作用力(力矩)时,常常要用到欧拉流场动量(矩)方程式。
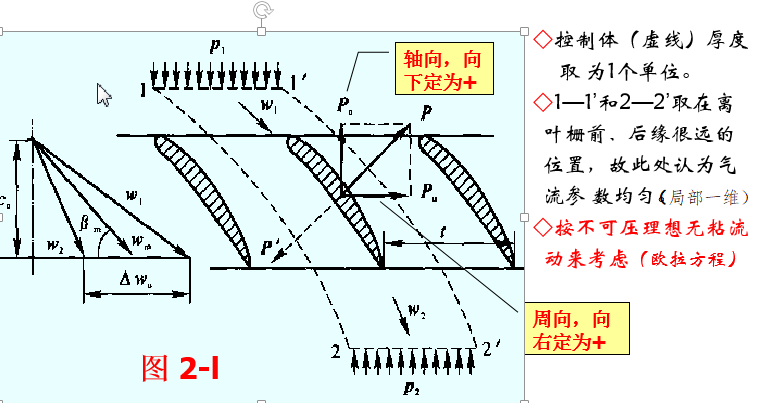
例如,对平面叶栅建立控制面流场动量方程分量式可以做叶片受力解析:
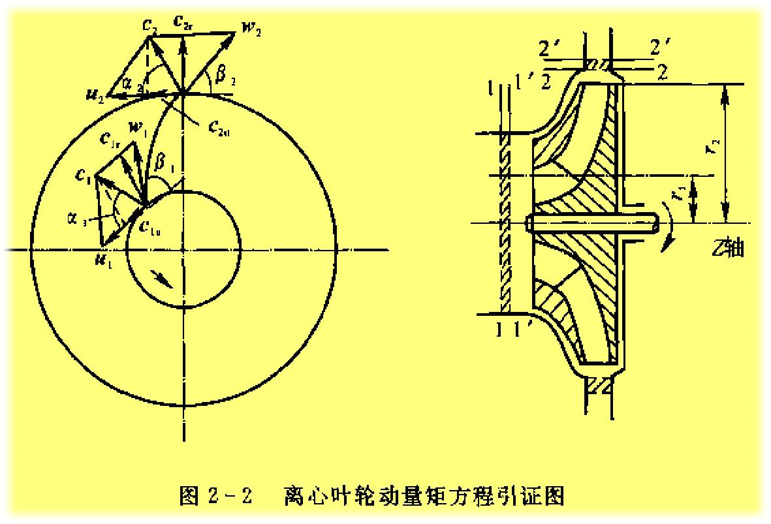
对离心叶轮流场控制体建立动量矩方程也能做所受力矩解析: