2.1.1 空间与地理空间的概念

从地理学角度看，空间可以认为是地表各种物质形态的分布场所。

一般认为，地理空间（Geographic Space）的范围上至大气电离层、下至地幔莫霍面，是地球上大气圈、水圈、生物圈、岩石圈和土壤圈交互作用的区域。地球上最复杂的物理过程、化学过程、生物过程和生物地球化学过程均发生在地理空间中；同时，地理空间也是人类活动频繁发生的区域，是人地关系中最为复杂和紧密的区域。

2.1.2 地理空间的数学建构

1. 自然表面

非常复杂，难以用一个简洁的数学表达式描述出来，不适合于数字建模。在该表面上进行长度、面积、体积、方向等的量测都面临非常大的困难。

2. 物理表面

假设当海水处于完全静止的平衡状态时，将海平面延伸到所有大陆下部，形成一个与地球重力方向处处正交的连续、闭合的水准面，这就是大地水准面。大地水准面所围成的球体即为大地体。

由于地球内部质量不均，重力线并不全都指向地心，因此大地水准面也仍然是一个具有高低起伏的不规则表面，不能用数学模型来进行定义和表达。

3. 数学表面

大地水准面很接近绕地球自转轴旋转的椭球体，所以在大地测量和地图制图中就采用旋转椭球体来代替大地体，通称地球参考椭球体。

大量的研究结果表明，赤道扁率比极地扁率小得多。因此为了便于计算，通常采用双轴椭球体又称为旋转椭球体，相当于将一个椭圆绕地轴旋转所形成的椭球体。

地球椭球体的三要素:a长半径（赤道半径）;C短半径（极半径);f扁率。

由于测定者、计算年代、采用的测定方法以及测定地区的不同，对椭球体的描述也不尽相同。

我国在1952年以前采用海福特（Hayford）椭球体，从1953年起改用前苏联的克拉索夫斯基（Krasovsky）椭球体，1978年开始决定采用1975年第十六届国际大地测量及地球物理联合会（IUGG/IAG）推荐的新的地球椭球体，称为IAG75椭球体，而目前GPS定位所采用的椭球体为1984年第十七届国际大地测量及地球物理联合会推荐的WGS84椭球体。

2.1.3 地理空间坐标系的建立

1. 地理坐标系

地理坐标系是为了确定地面点在地球椭球体表面的位置而定义的空间参照系，主要用经纬度来表示。

我国:“1954年北京坐标系”、“1980西安坐标系”、“2000国家大地坐标系”（ChinaGeodetic Coordinate System 2000，CGCS2000）。

2. 平面坐标系

依据旋转椭球体参数，采用一定的地图投影变换方法，将球面空间转换成平面空间，建立平面坐标系，形成球面上点与平面上点的一一对应关系。

平面坐标有良好的视觉感，并易于进行距离、方向、面积等空间参数的量算，以及进一步的空间数据处理和分析。

 我国国家基本比例尺地形图中的大中比例尺地图，一律采用高斯-克吕格（Gauss-Kruger）投影——横轴等角切椭圆柱投影（图2.6）。其中1:1万比例尺的地形图采用经差3度分带，1:2.5万～1:50万的采用经差6度分带（图2.7）。在每一个投影带内布置平面直角坐标系统。

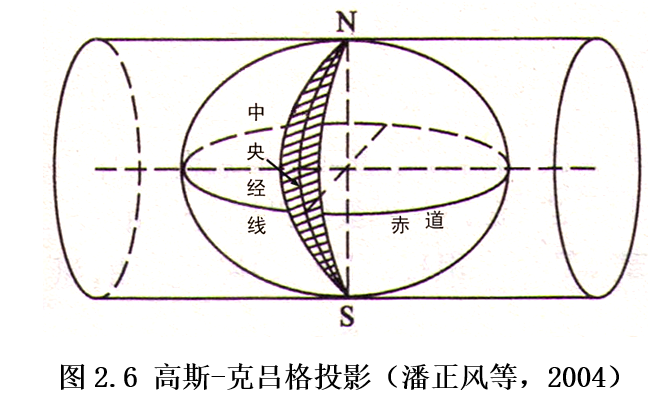
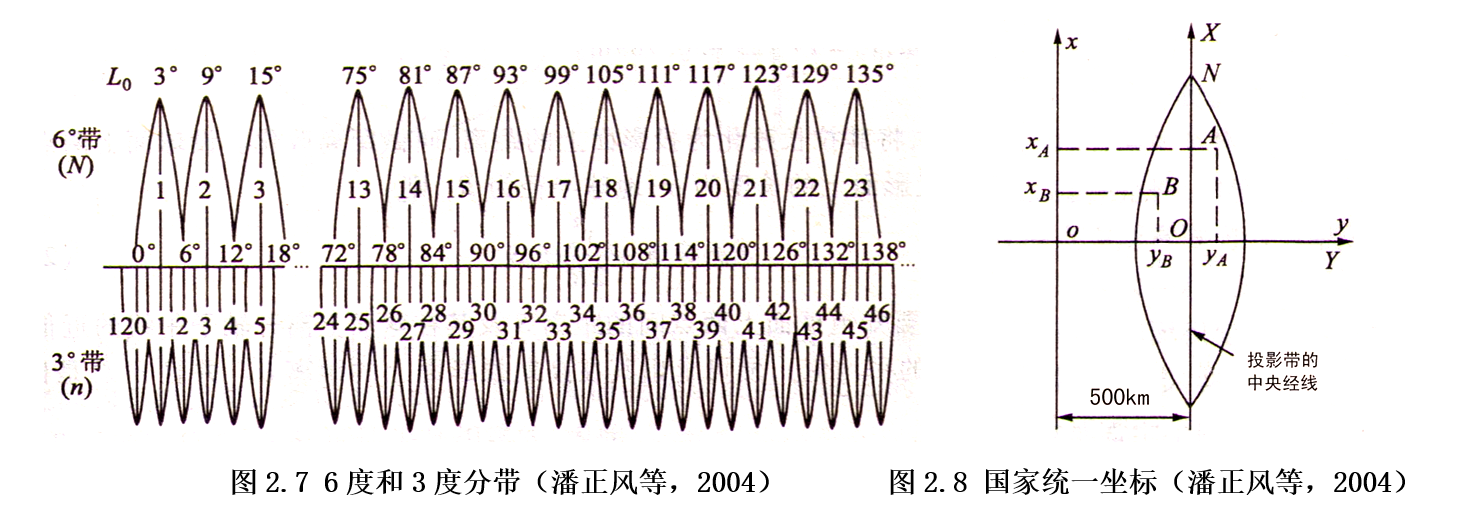
3. 高程系

高程是指由高程基准面起算的地面点的高度。

高程基准面是根据多年观测的平均海水面来确定的。

新中国成立以后，我国利用青岛验潮站1950～1956年的观测记录，确定黄海平均海水面为全国统一的高程基准面，并且在青岛观象山埋设了永久性的水准原点，以黄海平均海水面建立起高程控制系统，称为

“1956年黄海高程系”：采用1952～1979年的潮汐观测数据，水准原点的高程为72.289米。

“1985国家高程基准”：采用1952～1979年的潮汐观测数据，水准原点的新高程为72.260米。       

2.1.4 地理空间距离的度量

地理空间中两点间的距离有两种度量方法：一种是沿着真实的地球表面进行的，另一种是沿旋转椭球体表面进行的。

1）欧几里德距离：在较小的地理空间中，采用平面直角坐标系确定的距离。

2）曼哈顿距离：城市A、B两点在南北方向上的距离加上东西方向上的距离，相当于直角三角形两个直角边的距离之和。也称为出租车距离。

3）时间距离：采用从城市A到城市B所需要的时间来量度。

4）辞典距离：在一个固定的地名册中，两地位置之间的绝对差值（页数与行数）。

2.1.5 地理空间的拓扑关系

拓扑（Topology）:“形状的研究”。拓扑学是几何学的一个分支，它主要研究那些经过特定变换后仍然保持不变的几何属性——拓扑属性，这些变换包括拉伸、压缩等。

拓扑变换：把欧氏平面(橡皮)任意地被拉伸、压缩，但是不能够被扭转以及折叠，其表面上有由结点、弧段和多边形组成的任何可能的图形。

拓扑属性：拓扑变换过程中保持不变属性。点与线、面之间的位置关系；线与面之间的有关系；面与面之间的关系等

非拓扑属性：拓扑变换过程中发生变化的属性。线的长度和方向、面的周长和面积等

拓扑关系的三个类型：

  1）拓扑邻接关系：存在于空间图形同类元素之间的拓扑关系。

  2）拓扑关联关系：存在于空间图形不同类元素之间的拓扑关系。

  3）拓扑包含关系：空间图形同类但不同级别元素之间的拓扑关系。

三个重要的拓扑概念：

1）连接性：弧段与结点的拓扑关系体现了连接性。

2）多边形区域定义：多个弧段首尾相连构成了多边形的内部区域。多边形与弧段之间的拓扑关系体现了多边形区域的定义。

3）邻接性：邻接性反映弧段的左与右的拓扑关系，而这种关系是通过定义弧段的左右边以及弧段的方向来确定，也就是说，计算机要判断弧段两边的邻接关系，就必须明确弧段的方向以及在该方向上左右的多边形。

空间数据的拓扑关系研究的意义：

1）拓扑关系清晰地反映了地理实体之间的逻辑关系。通过它不需要利用坐标或距离，就可以确定一种空间实体相对于另一种空间实体的位置关系，它比几何数据有更大的稳定性，不随地图投影的变化而变化。

2）利用拓扑关系有利于空间要素的查询。例如一条公路穿过哪些地区；某县与哪些县邻接；某湖泊周围的土地类型有哪些等。

3）可以利用拓扑数据作为工具，重建地理实体。例如根据弧段构建多边形；根据车站与公交线路构建公交网络等。

此外，拓扑关系还可以为数据错误检查、空间数据编辑、属性数据输入、空间分析功能的实现等方面提供方便。

本节视频