MATLAB在频域分析中的应用

一、目的

1、掌握频域分析基本原理，matlab复数运算与相量图函数；

2、掌握多项式运算；

3、掌握积分函数；

4、了解最优化问题求解方法。

二、原理

1、复数运算与相量图函数

1）常用的复数运算函数

real(A)：求复数或复数矩阵A的实部；

imag(A)：求复数或复数矩阵A的虚部；

abs(A)：求复数或复数矩阵A的模；

conj(A)：求复数或复数矩阵A的共轭；

angle(A)：求复数或复数矩阵A的相角，单位为弧度。

需要注意MATLAB三角函数（sin、cos、tan等）计算应用弧度、

反三角函数（asin、acos、atan等）返回参数单位也是弧度。

2）compass 函数：绘制向量图

调用格式：compass([I1,I2,I3…])，引用参数为相量构成的行向量

3）绘制幅频特性和相频特性

方法一，将sàjω,利用Matlab编程实现

方法二，采用传递函数和频率特性的方法

方法三，采用bode 函数：绘制波特图

调用格式：bode(A，B)

                    A，B分别为网络函数分子和分母系数行向量

2、多项式运算

1）roots函数：求多项式函数的根

调用格式：r= roots(p)

p是多项式系数形成的行向量，系数按降序排列。

r为函数的根，是一个列向量。

2）poly函数：已知多项式函数的根，用以求多项式系数

调用格式：p= poly (r)

    r是多项式的根形成的列向量。

    p返回多项式系数行向量。

3、最优化问题求解

1）fminbnd：求单变量非线性函数极小值点

调用格式：

[X,FVAL,EXITFLAG,OUTPUT]=fminbnd(FUN,x1,x2,OPTIONS,P1,P2,...)

2）fminunc：拟牛顿法求多变量函数极小值点

调用格式：

[X,FVAL,EXITFLAG,OUTPUT,GRAD,HESSIAN]=fminunc(FUN,X0,OPTIONS,P1,P2,...)

3）fminsearch：采用Nelder-Mead单纯形法求多变量函数极小值点

调用格式：

[X,FVAL,EXITFLAG,OUTPUT]=fminsearch (FUN, X0, OPTIONS, P1,P2,...)

4、积分函数

1）trapz：采用梯形公式计算积分。

调用格式：trapz(X，Y)

X表示横坐标向量，Y为对应的纵坐标向量。要求X与Y的长度必须相等

2）quad：采用自适应Simpson算法积分。

调用格式：quad(‘fun’,a,b)

           计算被积函数fun在[a,b]区间的积分

三、内容

1、学习

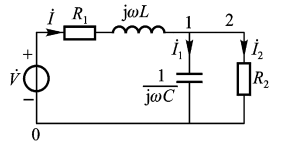
1）正弦稳态电路的基本计算

如图所示电路，已知R=5Ω，wL=3Ω，1/wC=2Ω，uc=10∠30°V，求Ir，Ic，I和UL,Us。并画出其向量图。

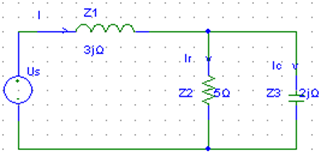
 程序如下：

>>Z1=3*j;Z2=5;Z3=-2*j;Uc=10*exp(30j*pi/180);

Z23=Z2*Z3/(Z2+Z3);Z=Z1+Z23;

Ic=Uc/Z3,Ir=Uc/Z2,I=Ic+Ir,U1=I*Z1,Us=I*Z

disp('Uc   Ir Ic   i   U1  Us')

disp('幅值'),disp(abs([Uc,Ir,Ic,I,U1,Us]))

disp('相角'),disp(angle([Uc,Ir,Ic,I,U1,Us])*180/pi)

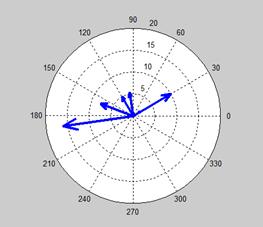
ha=compass([Uc,Ir,Ic,I,U1,Us]);

set(ha,'linewidth',3)

Ic =

 -2.5000 + 4.3301i

Ir =

   1.7321 +1.0000i

I =

 -0.7679 + 5.3301i

U1 =

 -15.9904 - 2.3038i

Us =

 -7.3301 + 2.6962i

Uc  Ir  Ic   i  U1   Us

幅值

     10.0000    2.0000   5.0000    5.3852  16.1555    7.8102

相角

     30.0000  30.0000  120.0000   98.1986 -171.8014  159.8056

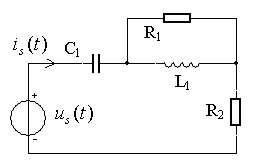
2）正弦稳态电路的功率计算

已知R1=40Ω，R2=60Ω，C1=1uF，L1=0.1mH， V。

求电压源的平均功率、无功功率和视在功率。

解：（1）采用相量法的求解步骤：

        。

（2）编写MATLAB程序：

Us=40/2^0.5; wo=1e4;  R1=40;  R2=60; C=1e-6;  L=0.1e-3;

ZC=1/(j*wo*C);   %C1容抗

ZL=j*wo*L;   %L1感抗

ZP=R1*ZL/(R1+ZL); %R1，L1并联阻抗

ZT=ZC+ZP+R2;

Is=Us/ZT;

Sg=Us*conj(Is); %复功率

AvePower=real(Sg)  %平均功率

Reactive=imag(Sg)  %无功功率

ApparentPower=Us*abs(Is) %视在功率

（3）运行结果：

AvePower = 3.5825；       Reactive =-5.9087；

ApparentPower = 6.9099

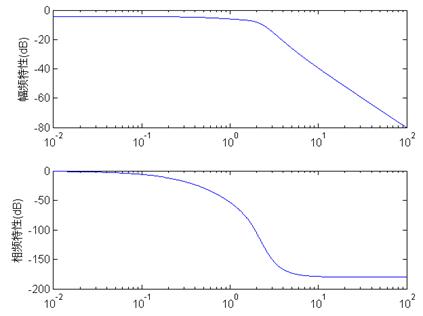
3）绘制幅频特性和相频特性

已知网络函数为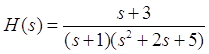，作幅频特性和相频特性。

解：方法一，将s—> jω,利用Matlab编程实现

w=0:0.01:100;

Hs=(j*w+3)./(j*w+1)./((j*w).^2+2*j*w+5);

Hs_F=20*log10(abs(Hs));          %幅频特性用dB表示

Hs_A=angle(Hs)*180/pi;      %将弧度转化为角度表示

subplot(2,1,1);

semilogx(w,Hs_F)          %横坐标以对数坐标表示的半对数曲线

ylabel('幅频特性(dB)');

subplot(2,1,2);

semilogx(w,Hs_A)

ylabel('相频特性(dB)')

方法二，采用传递函数和频率特性

num=[1 3];                 %   num  传递函数的分子多项式

den=[1 3 7 5];       %   den 传递函数的分母多项式

w=0:0.01:100;            %  w 角频率

g=freqs(num,den,w);     % g传递函数、freqs(num,den,w)频率特性

mag=20*log10(abs(g));    %mag=abs(g)传递函数幅频特性的幅值

semilogx(w,mag)

% plot(w,mag)

xlabel('Frequency-rad/s');

ylabel('Magnitude');

方法三， bode 函数：绘制波特图

A=[1 3];

B=conv([1 1],[1 2 5])

bode(A,B)

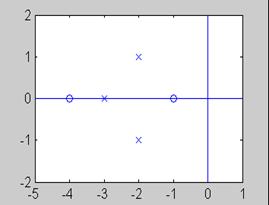
4）用roots求多项式函数的根，绘制零极点图。

已知网络函数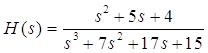，绘制零极点图。

解：程序

p=[1 5 4];

ld=roots(p)

p=[1 7 17 15];

jd=roots(p)

axis xy;

plot(real(ld),imag(ld),'o');

hold on;

plot(real(jd),imag(jd),'x');

axis([-5 1 -2 2])

line([-5,1],[0,0])

line([0,0],[2,-2])

执行程序结果：

5）采用trapz梯形公式计算积分，求有效值

设某周期性矩形脉冲电流i(t)如图所示。其中脉冲幅值mA

周期T = 6.28，脉冲宽度。求i(t)有效值。

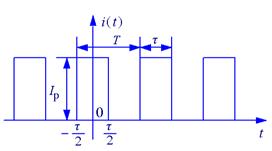
解：根据有效值的定义

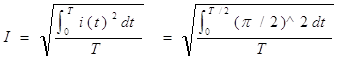，Matlab程序：

clear;

T=6.28;

t=0:1e-3:T/2; %));        %1e-3为计算步长;

it=zeros(1,length(t));    %开设电流向量空间;

it(:)=pi/2;        %电流向量幅值;

I=sqrt(trapz(t,it.^2)/T)    %求电流均方根，得有效值

结果：I＝1.1107(mA)

6）采用quad自适应Simpson算法积分，求有效值

已知某二端网络端口电压、电流表达式：，，求有效值、电路的平均功率和功率因数。

解：Matlab程序

T = 2/100;      % 周期

a = 0;              % 积分区间的下限

x = 0:0.01:1;

t = x.*T;

v_int = quad('(80*cos(100*pi*t + 45*pi/180)).^2', a,T);

                         %求电压函数的平方在(a,T)的积分

v_rms = sqrt(v_int/T)       % 求得电压有效值

i_int = quad('(10*cos(100*pi*t +30.0*pi/180)).^2',a,T);

i_rms = sqrt(i_int/T);         % 求得电流有效值

p_int = quad('(10*cos(100*pi*t +30.0*pi/180)).*(80*cos(100*pi*t + 45*pi/180))', a, T);

p_ave = p_int/T           % 平均功率

pf = p_ave/(i_rms*v_rms)     %功率因数

结果： 

         v_rms= 56.5685

         p_ave=  386.3703

         pf =0.9659

7）采用fminsearch求多变量函数极小值点

对于下图所示电路，，改变电感L以调整电路并知道存在合适R、L，使得 。试确定功率因数最大时的R、L值。

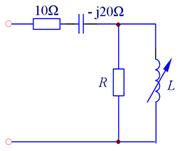
解：（1）分析

总阻抗

当Z虚部为零时，

因此，求解问题转化为：

（2）Matlab程序

[X,Fval]=fminsearch('abs(1000*x(2)*x(1)^2/(x(1)^2+(1000*x(2))^2)-20)',[10,0.2])

（3）结果

X =

  40.0000    0.0400

Faval =

 7.5276e-007

即R=40Ω，L=0.04H，此时阻抗Z虚部近似等于零，

 

2、上机操作

向量方程及其求解

（1）function p=degree(c)   % degree.m

p=angle(c)*180/pi;

（2）function [c,d]=cmplx(m,d)   % cmplx.m

switch(nargin)

case nargin>2

error('Too many input arguments')

case 2

       c=m.*exp(i*d*pi/180);

       d=m+i*d;

case 1

           [nr,nc]=size(m);

vname=inputname(1);

if isempty(vname)

vname='ans';

end

           c=abs(m);

           d=degree(m);

fprintf('%s=\n',vname)

           m=[c,d];

for k=2:nc

temp=m(:,k);

                n=nc+k-1;

m(:,k)=m(:,n);

m(:,n)=temp;

end

disp(m);

end             %运行以下程序时首先运行此程序

 

cmplx(5,53.13)

3.0000 + 4.0000i

[c1,c2]=cmplx(5,53.13)

c1 =3.0000 + 4.0000i, c2 =5.0000+53.1300i

cmplx(3 + 4i)

ans=5.0000  53.1301

[m,d]=cmplx(3 + 4i)

m =5, d =53.1301

 

运行程序1：%求i和Us

i1=10;i2=j*10;l=j*10;r=10;

i=i1+i2;

Us=i*l+i1*r;

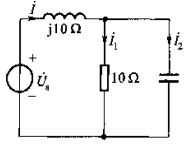
运行结果：i

i =

 10.0000 +10.0000i

>> Us

Us =

           0 +1.0000e+002i

运行程序2：ex8_1_1.m

   r1=10;

   l=0.5;

   r2=1000;

   c=10e-6;

    v=100;w=314;

    y1=1/(r1+j*w*l);

    v1=y1*v/(y1+j*w*c+1/r2);

    i0=y1*(v-v1);

    i1=j*w*c*v1;

    i2=v1/r2;

cmplx(v1);cmplx(i0);cmplx(i1);cmplx(i2);

运行结果：

v1=

    181.7268 -20.0215

i0=

    0.5989  52.3133

i1=

    0.5706  69.9785

i2=

0.1817  -20.0215

运行程序3：ex8_1_2.m

r1=10;

l=0.5;r2=1000;

c=10e-6;v=100;

w=314;

a=[r1+j*w*l+1/(j*w*c),-1/(j*w*c);-1/(j*w*c),r2+1/(j*w*c)];

b=[v;0];

x=a\b;

i0=x(1);i2=x(2);

v1=i0-i2;

v1=i1/(j*w*c);

cmplx(v1);cmplx(i0);cmplx(i1);cmplx(i2);

运行结果与ex8_1_1.m的相同。

四、任务（作业）

1．邱关源、罗先觉.电路（第五版）教材中第8~9章习题。