MATLAB在动态电路时域分析中的应用

一、目的

1、掌握动态电路的时域分析方法；

2、掌握动态电路的MATLAB计算方法；

3、掌握微分方程的MATLAB求解方法。

二、原理

1、动态电路计算

MATLAB为求解常微分方程提供了一组配套齐全，结构完整的指令。包括常微分方程解算指令solver，调用的ODE文件格式指令（MATLAB中计算导数的M函数文件称为ODE文件）。“ode23”是采用2、3阶龙格-库塔法求解常微分方程调用的ODE文件，“ode45”是采用4、5阶龙格-库塔法求解常微分方程调用的ODE文件。

利用MATLAB指令具体求解动态电路的步骤：

1）应用支路法或回路法等写出电路的一阶微分方程组和相应的初始条件，这里变量指定用y表示。

2）编写能计算导数的M函数文件，最简易的编写方法是把y，t作为输入宗量。

3）将编写好能计算导数的M函数文件（ODE函数文件）和初始值供微分方程解算指令solver调用，运行程序后就可得到变量y及其导数在指定时间上的数值解。

solver解算指令的使用格式为

[t,YY]= solver('F',tspan,y0)

这是用MATLAB求解微分方程最简单的格式。实际计算时，solver应是具体指令名如ode45等，这里输入宗量F是ODE函数文件名；当tspan被赋予二元向量[t0, tf]时，tspan用来定义求数值解的时间区间。输入宗量y0表示初始值的列向量。

三、内容

1、用三要素法求解一阶动态电路

电路如图所示，已知R1=3Ω，R2=12Ω，R3=6Ω，C=1F；Us=18V，is=3A，在t<0时，开关S位于“1”，电路已处于稳态。

（1）t=0时，开关S闭合到“2”，求uc（t），iR2（t），并画出波形。

（2）若经10s，开关S又复位到“1”，求uc（t）, iR2（t）,并画出波形。

解：MATLAB程序

clear all

R1=3;us=18;is=3;R2=12;R3=6;C=1;

uc0=-12;ir20=uc0/R2;ir30=uc0/R3;

ic0=is-ir20-ir30;

ir2f=is*R3/(R2+R3);

ir3f=is*R2/(R2+R3);

ucf=ir2f*R2;icf=0;

t=[-2-eps,0-eps,0+eps,0:9,10-eps,10+eps,11:20];

figure(1),plot(t),grid

uc(1:3)=-12;ir2(1:3)=3;

T=R2*R3/(R2+R3)*C;

uc(4:14)=ucf+(uc0-ucf)*exp(-t(4:14)/T);ir2(4:14)=ir2f+(ir20-ir2f)*exp(-t(4:14)/T);

uc(15)=uc(14);ir2(15)=is;

ucf2=-12;ir2f=is;

T2=R1*R3/(R1+R3)*C;

uc(15:25)=ucf2+(uc(15)-ucf2)*exp(-(t(15:25)-t(15))/T2);

ir2(15:25)=is;

figure(2)

subplot(2,1,1);h1=plot(t,uc);

grid,set(h1,'linewidth',2)

subplot(2,1,2);h2=plot(t,ir2);

grid,set(h2,'linewidth',2)

程序所得的结果：

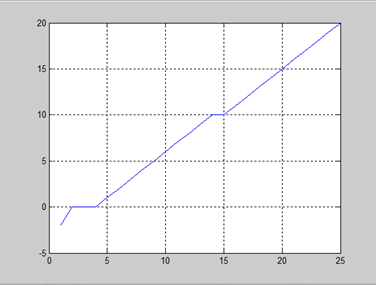
图时间与其数组下标的关系

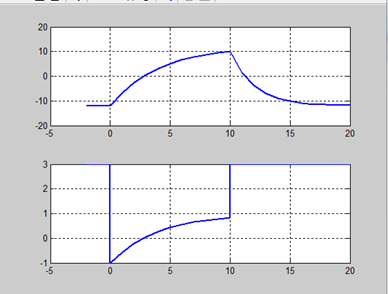
uc（t），iR2（t）波形

2、用微分函数diff(x)/diff(t)求解动态电路

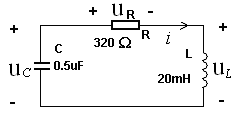
已知RLC串联电路的零输入响应

作出u_R、u_L、u_C的波形，并求u_C(0₊)、 u_L(0₊)

解：（1）分析

  

（2）MATLAB程序

t=1e-9:1e-6:0.600001e-3;

io=50e-3*exp(-8000*t).*(cos(6000*t)+2*sin(6000*t));   

                               %注意，数组元素相乘要使用.*

UR=320*io;                     %电阻电压

UL=20e-3*diff(io)./diff(t);    %diff：相邻元素的差，

                              %diff(io)./diff(t)：数值微分

UL=[UL,0];      %数值微分后UL数组元素个数减1，为了保证与t元素个数一致，须补充1位。因补充数值为0;

UC=UR+UL;

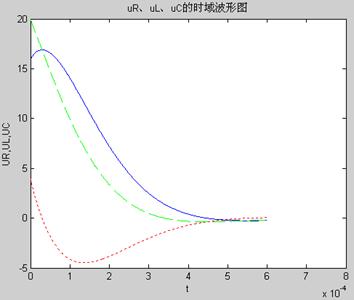
plot(t,UR,t,UL,t,UC)

title('uR、uL、uC的时域波形图');      %加图形标题

xlabel('t');                 %加X轴说明

ylabel('UR,UL,UC');          %加Y轴说明

运行程序得u_R、u_L、u_C的时域波形图如下图所示：

 

3、用solver解算指令求解二阶动态电路

二阶动态电路如图所示，已知Us=10V，R1=4Ω，R2=0.2Ω，C=1F； L=1H，，t=0时，开关S闭合，试绘出uc（t）波形。

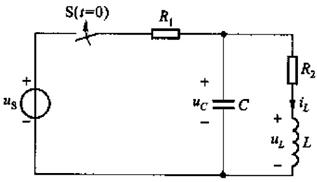
解：电路的状态方程表示如下：

应用MATLAB，在命令菜单中输入edit命令进入程序编辑器，编辑文件。电路的一阶微分方程组编写的MATLAB文件DYDt50.m为

function yd=DYDt50(t,y)

U=10;

R1=4;

R2=0.2;

C=1;

L=1;

yd=[-(1/(R1*C))*y(1)-(1/C)*y(2)+(1/(R1*C))*U;

    (1/L)*y(1)-(R2/L)*y(2)];

solver解算指令的使用格式程序C_5.m为

tspan=[0,40];        %  求解数值解的时间区间

y0=[0;0];            %  电路变量的初始值

[t,YY]=ode45('DYDt50',tspan,y0);     %     solver解算指令的使用格式

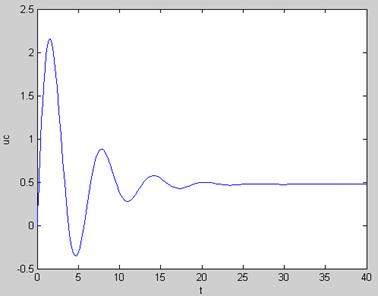
plot(t,YY(:,1));                      %   绘制uc的时域波形图

xlabel('t'),ylabel('uc');

调用solver解算指令的使用格式程序，运行C_5.m程序得uc（t）的时域波形图如下图所示：

solver解算指令的使用格式程序C_5_1.m为

tspan=[0,40];        %  求解数值解的时间区间

y0=[0;0];            %  电路变量的初始值

[t,YY]=ode23('DYDt50',tspan,y0);     %     solver解算指令的使用格式

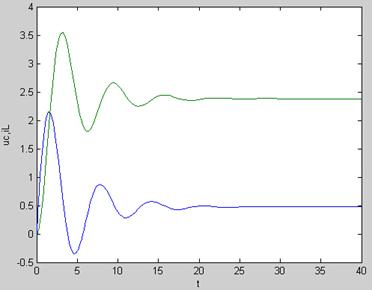
plot(t,YY);                        %     绘制uc和iL的时域波形图

xlabel('t'),ylabel('uc,iL');

调用solver解算指令的使用格式程序，运行C_5_1.m程序得uc（t）和iL（t）的时域波形图如下图所示：

 

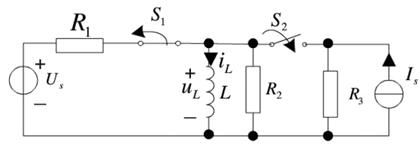
四、任务（作业）

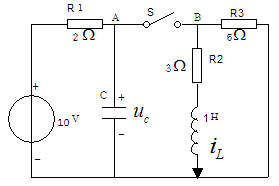
1．电路如图所示，已知R1=1Ω，R2=3Ω，R3=2Ω，Us=10V，Is=3A， L=2H。

（1）在t=0时，开关S1闭合，在开关动作前电路已处于稳态，试求：t≥0时的，并画出它们的波形。

（2）在经过10s后，开关S1打开，S2闭合，求此时的，并画出它们的波形。

 

2．如图所示电路，在开关S打开前电路已处于稳态，求S打开后的电压u_AB（t）。

C=1uF