MATLAB绘图操作
一、目的
1、掌握MATLAB绘制二维图形的常用函数;
2、掌握MATLAB绘制三维图形的常用函数;
3、掌握MATLAB绘制图形的辅助操作。
二、原理
1、二维数据曲线图
(1) 绘制单根二维曲线 plot(x,y);
(2) 绘制多根二维曲线 plot(x,y) 当x是向量,y是有一维与x同维的矩阵时,则绘制多根不同颜色的曲线。当x,y是同维矩阵时,则以x,y对应列元素为横、纵坐标分别绘制曲线,曲线条数等于矩阵的列数。
(3) 含有多个输入参数的plot函数 plot(x1,y1,x2,y2,…,xn,yn)
(4) 具有两个纵坐标标度的图形 plotyy(x1,y1,x2,y2)
2、图形标注与坐标控制
1)title (图形名称);
2)xlabel(x轴说明)
3)ylabel(y轴说明)
4)text(x,y图形说明)
5)legend(图例1,图例2,…)
6)axis ([xmin xmax ymin ymax zmin zmax])
3、图形窗口的分割
subplot(m,n,p)
4、三维曲线
plot3(x1,y1,z1,选项1,x2,y2,选项2,…,xn,yn,zn,选项n)
5、三维曲面
mesh(x,y,z,c) 与surf(x,y,z,c)。一般情况下,x,y,z是维数相同的矩阵。X,y是网格坐标矩阵,z是网格点上的高度矩阵,c用于指定在不同高度下的颜色范围。
6、图像处理
1) imread和imwrite函数这两个函数分别用于将图象文件读入matlab工作空间,以及将图象数据和色图数据一起写入一定格式的图象文件。
2) image和imagesc函数这两个函数用于图象显示。为了保证图象的显示效果,一般还应使用colormap函数设置图象色图。
三、内容
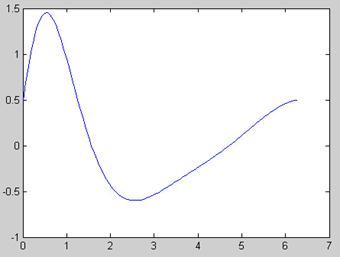
1、设![]() ,在x=0~2π区间取101点,绘制函数曲线。
,在x=0~2π区间取101点,绘制函数曲线。
x=linspace(0,2*pi,101);
y=(0.5+3*sin(x)./(1+x.*x)).*cos(x);
plot(x,y)
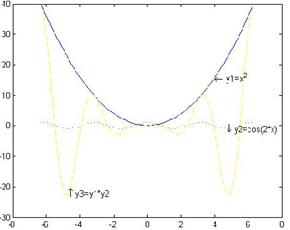
2、已知y1=x2,y2=cos(2x),y3=y1*y2,完成下列操作:
(1)在同一坐标系下用不同的颜色和线型绘制三条曲线;
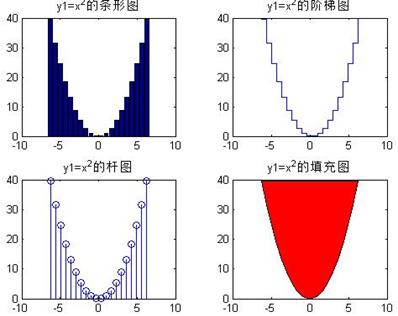
(2)分别用条形图、阶梯图、杆图和填充图绘制三条曲线。
2.1>
x=linspace(-2*pi,2*pi,100);
y1=x.^2;
y2=cos(2*x);
y3=y1.*y2;
plot(x,y1,'b-',x,y2,'r:',x,y3,'y--');
text(4,16,'\leftarrowy1=x^2');
text(6*pi/4,-1,'\downarrowy2=cos(2*x)');
text(-1.5*pi,-2.25*pi*pi,'\uparrow y3=y1*y2');
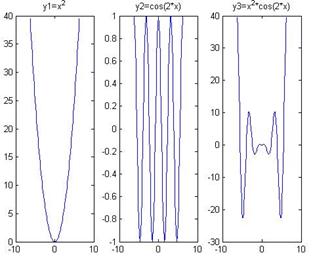
2.2>
x=linspace(-2*pi,2*pi,100);
y1=x.^2;
y2=cos(2*x);
y3=y1.*y2;
subplot(1,3,1);
plot(x,y1);
title('y1=x^2');
subplot(1,3,2);
plot(x,y2);
title('y2=cos(2*x)');
subplot(1,3,3);
plot(x,y3);
title('y3=x^2*cos(2*x)');
2.3>
x=linspace(-2*pi,2*pi,20);
y1=x.^2;
subplot(2,2,1);
bar(x,y1);
title('y1=x^2条形图 ');
subplot(2,2,2);
stairs(x,y1);
title('y1=x^2阶梯图 ');
subplot(2,2,3);
stem(x,y1);
title('y1=x^2杆图 ');
subplot(2,2,4);
fill(x,y1,'r');
title('y1=x^2填充图 ');
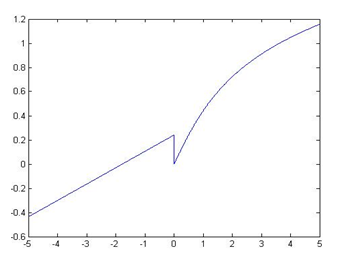
3、已知
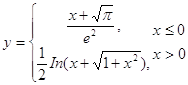
在-5<=x<=5区间绘制函数曲线。
x=-5:0.01:5
y=(x+sqrt(pi))/exp(2).*(x<=0)+1/2*log(x+sqrt(1+x.^2)).*(x>0)
plot(x,y)
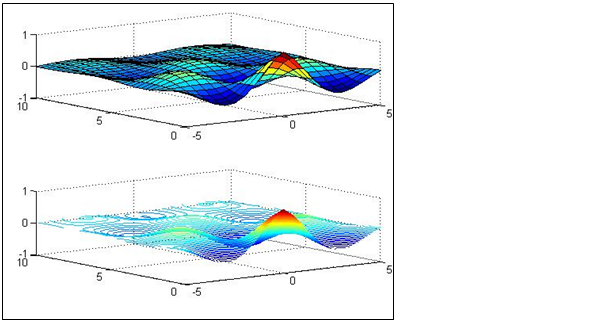
4、绘制函数的曲面图和等高线
![]()
其中x的21个值均匀分布在[-5,5]范围,y的31个值均匀分布在[0,10],要求使用subplot(2,1,1)和subplot(2,1,2)将产生的曲面图和登高图画在同一个窗口上。
x=linspace(-5,5,21);
y=linspace(0,10,31);
[x,y]=meshgrid(x,y);
z=cos(x).*cos(y).*exp(-sqrt(x.^2+y.^2)/4);
subplot(2,1,1);
surf(x,y,z);
subplot(2,1,2);
contour3(x,y,z,50);
四、任务(作业)
1. 完成实验内容中的图像的显示;
2. 验证实验内容中所显示图像的正确性。