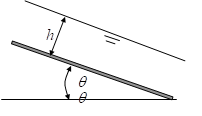
带有自由面的粘性不可压缩流体在倾斜平板上由于重力的作用而发生运动。设：平板无限大，与水平面的倾角为θ，流体的深度为h，作定常层流运动。求：速度分布、平均流速及作用在平板上的摩擦力。

一无限长的平板沿y=0放置，一强度为m的点源位于平板上部，距平板距离为h。试求：（1）写出平板以上区域内的复势；（2）利用伯努利方程求解平板以上表面的压力分布；（3）求流体对平板的总压力。设平板下部压强等于流体的滞止压强。

不可压缩流体在无界流场中有一对方向相反、强度相等为Τ的线涡，分别置于（0，h）和（0，-h）两点。这时有无穷远速度为V∞的均匀来流恰好使得这两个涡线停滞不动。求其流线方程。