信号检测理论

张烨

目录

  • 1 信号检测与估计概论
    • 1.1 引言
    • 1.2 信号处理发展概况
    • 1.3 信号的随机性及其统计方法
    • 1.4 信号检测与估计理论概述
    • 1.5 内容编排和建议
  • 2 信号检测与估计理论的基础知识
    • 2.1 引言
    • 2.2 随机变量、随机矢量及其统计描述
      • 2.2.1 随机变量的基本概念
      • 2.2.2 随机变量的概率密度函数
      • 2.2.3 随机变量的统计平均量
      • 2.2.4 一些常用的随机变量
      • 2.2.5 随机矢量及其统计描述
      • 2.2.6 随机变量的函数
      • 2.2.7 随机变量的特征函数
      • 2.2.8 随机矢量的联合特征函数
      • 2.2.9 统计量的统计特性
    • 2.3 随机过程及其统计描述
      • 2.3.1 随机过程的概念和定义
      • 2.3.2 随机过程的统计描述
      • 2.3.3 随机过程的统计平均量
      • 2.3.4 随机过程的平稳性
      • 2.3.5 随机过程的遍历性
      • 2.3.6 随机过程的正交性、不相关性和统计独立性
      • 2.3.7 平稳随机过程的功率谱密度
    • 2.4 复随机过程及其统计描述
      • 2.4.1 复随机过程的概率密度函数
      • 2.4.2 复随机过程的二阶统计平均量
      • 2.4.3 复随机过程的正交性、不相关性和统计独立性
      • 2.4.4 复高斯随机过程
    • 2.5 线性系统对随机过程的响应
      • 2.5.1 响应的平稳性
      • 2.5.2 响应的统计平均量
    • 2.6 高斯噪声、白噪声和有色噪声
      • 2.6.1 高斯噪声
      • 2.6.2 白噪声和高斯白噪声
      • 2.6.3 有色噪声
      • 2.6.4 随机过程概率密度函数表示法的说明
    • 2.7 信号和随机参量信号及其统计描述
      • 2.7.1 信号的分类
      • 2.7.2 随机参量信号的统计描述
      • 2.7.3 窄带信号分析
    • 2.8 窄带高斯噪声及其统计特性
      • 2.8.1 窄带噪声的描述
      • 2.8.2 窄带高斯噪声的统计特性
    • 2.9 信号加窄带高斯噪声及其统计特性
      • 2.9.1 信号加窄带噪声的描述
      • 2.9.2 信号加窄带高斯噪声的统计描述
  • 3 信号的统计检测理论
    • 3.1 引言
    • 3.2 信号统计检测理论的基本概念
      • 3.2.1 统计检测理论的基本模型
      • 3.2.2 统计检测的结果和判决模型
    • 3.3 贝叶斯准则
      • 3.3.1 平均代价的概念和贝叶斯准则
      • 3.3.2 平均代价C的表达式
      • 3.3.3 判决表示式
      • 3.3.4 检测性能分析
    • 3.4 派生贝叶斯准则
      • 3.4.1 最小平均错误概率准则
      • 3.4.2 最大后验概率准则
      • 3.4.3 极大极小准则
      • 3.4.4 奈曼-皮尔逊准则
    • 3.5 信号检测的性能
    • 3.6 M元信号的统计检测
      • 3.6.1 M元信号检测的贝叶斯准则
      • 3.6.2 M元信号检测的最小平均错误概率准则
    • 3.7 参量信号的统计检测
      • 3.7.1 参量信号统计检测的基本概念
      • 3.7.2 参量信号统计检测的方法
      • 3.7.3 广义似然比检验
      • 3.7.4 贝叶斯方法
    • 3.8 信号的序列检测
      • 3.8.1 信号序列检测的基本概念
      • 3.8.2 信号序列检测的平均观测次数
    • 3.9 一般高斯信号的统计检测
    • 3.10 复信号的统计检测
  • 4 信号波形的检测
    • 4.1 引言
    • 4.2 匹配滤波器
      • 4.2.1 匹配滤波器的概念
      • 4.2.2 匹配滤波器的设计
      • 4.2.3 匹配滤波器的主要特性
    • 4.3 随机过程的正交级数展开
      • 4.3.1 完备的正交函数集及确知信号的正交级数展开
      • 4.3.2 随机过程的正交级数展开
      • 4.3.3 随机过程的卡亨南.洛维展开
      • 4.3.4 白噪声情况下正交函数集的任意性
      • 4.3.5 参量信号时随机过程的正交级数展开
    • 4.4 高斯白噪声中确知信号波形的检测
      • 4.4.1 简单二元信号波形的检测
      • 4.4.2 一般二元信号波形的检测
      • 4.4.3 M元信号波形的检测
    • 4.5 高斯有色噪声中确知信号波形的检测
      • 4.5.1 信号模型及其统计特性
      • 4.5.2 信号检测的判决表示式
      • 4.5.3 检测系统的结构
      • 4.5.4 检测性能分析
      • 4.5.5 最佳信号波形设计
    • 4.6 高斯白噪声中随机参量信号波形的检测
      • 4.6.1 随机相位信号波形的检测
      • 4.6.2 随机振幅与随机相位信号波形的检测 （P219）
  • 5 信号的统计估计理论
    • 5.1 引言
      • 5.1.1 信号处理中的估计问题
      • 5.1.2 参量估计的数学模型和估计量的构造
      • 5.1.3 估计量性能的评估
    • 5.2 随机参量的贝叶斯估计
      • 5.2.1 常用代价函数和贝叶斯估计的概念
      • 5.2.2 贝叶斯估计量的构造
      • 5.2.3 最佳估计的不变性
    • 5.3 最大似然估计
      • 5.3.1 最大似然估计原理
      • 5.3.2 最大似然估计量的构造
      • 5.3.3 最大似然估计的不变性
    • 5.4 估计量的性质
      • 5.4.1 估计量的主要性质
      • 5.4.2 克拉美罗不等式和克拉美罗界
      • 5.4.3 无偏有效估计量的均方误差与克拉美罗不等式取等号 成立条件式中的 k(θ)或 k的关系
      • 5.4.4 非随机参量函数估计的克拉美-罗界
    • 5.5 矢量估计
      • 5.5.1 随机矢量的贝叶斯估计
      • 5.5.2 非随机矢量最大似然估计
      • 5.5.3 矢量估计量的性质
      • 5.5.4 非随机矢量函数估计的克拉美罗界
    • 5.6 一般高斯信号参量的统计估计
      • 5.6.1 线性观测模型
      • 5.6.2 高斯噪声中非随机矢量的最大似然估计
      • 5.6.3 高斯随机矢量的贝叶斯估计
      • 5.6.4 随机矢量的伪贝叶斯估计
      • 5.6.5 随机矢量的经验伪贝叶斯估计
    • 5.7 线性最小均方误差估计
      • 5.7.1 线性最小均方误差估计准则
      • 5.7.2 线性最小均方误差估计矢量的构造
      • 5.7.3 线性最小均方误差估计矢量的性质
      • 5.7.4 线性最小均方误差递推估计
      • 5.7.5 单参量的线性最小均方误差估计
      • 5.7.6 观测噪声不相关时单参量的线性最小均方误差估计
      • 5.7.7 观测噪声相关时单参量的线性最小均方误差估计
      • 5.7.8 随机矢量函数的线性最小均方误差估计
    • 5.8 最小二乘估计
      • 5.8.1 最小二乘估计方法
      • 5.8.2 线性最小二乘估计
      • 5.8.3 线性最小二乘加权估计
      • 5.8.4 线性最小二乘加递推计
      • 5.8.5 单参量的线性最小二乘估计
      • 5.8.6 非线性最小二乘估计
    • 5.9 信号波形中参量估计
      • 5.9.1 信号振幅的估计
      • 5.9.2 信号相位的估计
      • 5.9.3 信号频率的估计
      • 5.9.4 信号到达时间的估计
      • 5.9.5 信号频率和到达时间的同时估计
  • 6 信号波形的估计
    • 6.1 引言
      • 6.1.1 信号波形估计的基本概念
      • 6.1.2 信号波形估计的准则和方法
    • 6.2 连续过程的维纳滤波
      • 6.2.1 最佳线性滤波
      • 6.2.2 维纳霍夫方程
      • 6.2.3 维纳滤波器的非因果解
      • 6.2.4 维纳滤波器的因果解
    • 6.3 离散过程的维纳滤波
      • 6.3.1 离散的维纳霍夫方程
      • 6.3.2 离散维纳滤波器的z域解
      • 6.3.3 离散维纳滤波器的时域解
    • 6.4 正交投影原理
      • 6.4.1 正交投影的概念
      • 6.4.2 正交投影引理
    • 6.5 离散卡尔曼滤波信号模型
      • 6.5.1 离散状态方程和观测方程
      • 6.5.2 离散信号模型的统计特性
    • 6.6 离散卡尔曼滤波
      • 6.6.1 离散卡尔曼滤波的递推公式
      • 6.6.2 离散卡尔曼滤波的递推算法
      • 6.6.3 离散卡尔曼滤波的特点和性质
    • 6.7 状态为标量时的离散卡尔曼滤波
      • 6.7.1 状态为标量的离散状态方程和观测方程
      • 6.7.2 状态为标量的离散卡尔曼滤波
      • 6.7.3 有关参数的特点
    • 6.8 离散卡尔曼滤波的扩展
      • 6.8.1 白噪声情况下的一般信号模型滤波
      • 6.8.2 扰动噪声与观测噪声相关情况下的滤波
      • 6.8.3 扰动噪声是有色噪声下的滤波
      • 6.8.4 观测噪声是有色噪声下的滤波
      • 6.8.5 扰动噪声和观测噪声都是有色噪声下的滤波
    • 6.9 卡尔曼滤波的发散现象
    • 6.10 非线性离散状态估计
信号检测的性能

3.5  信号检测的性能


从前面的讨论可看出：不同准则的“最佳”性能指标，都与错误判决概率P(H1|H0)、正确判决概率P(H1|H1)有关，对此判决概率作进一步讨论。

似然比检验的判决表示式为

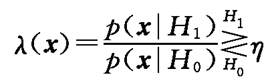                                          (3.5.1)

因为似然比函数亦是一随机变量，也就有自己的概率密度函数，根据概率论中的有关理论，似然比概率密度函数与观测信号的概率密度函数的关系有

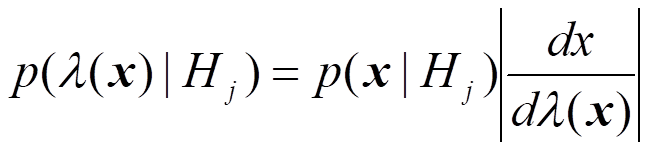
所以，判决概率可以表示为：

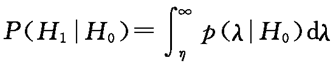                                                                  (3.5.2)


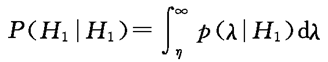                           (3.5.3)

显然，通过检测门限η，可将判决概率联系起来。

通常，似然比检验是可以化简的，结果的一般形式为：

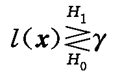
或

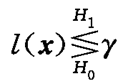                                                               (3.5.4)

这样，判决概率又可表示为

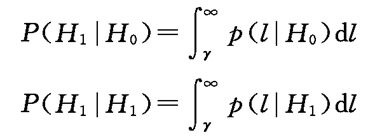
或


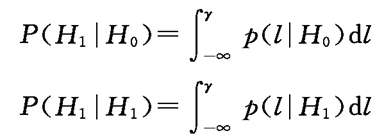
举例说明(见讲义P89---P93) ：

以例3.3.1中的结果，检验统计量为 

检测门限为

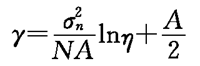                                                                                                (3.5.10)


在假设H0、H1下，l(x)均服从高斯分布，可得到其判决概率为

                      (3.5.11)

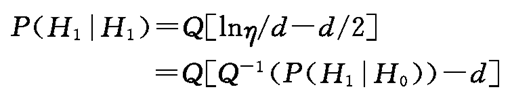                   (3.5.12)

其中d 2为功率信噪比：

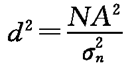                                                            (3.5.13)

而

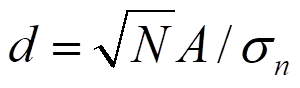
称为幅度信噪比。

判决概率如图3.11所示









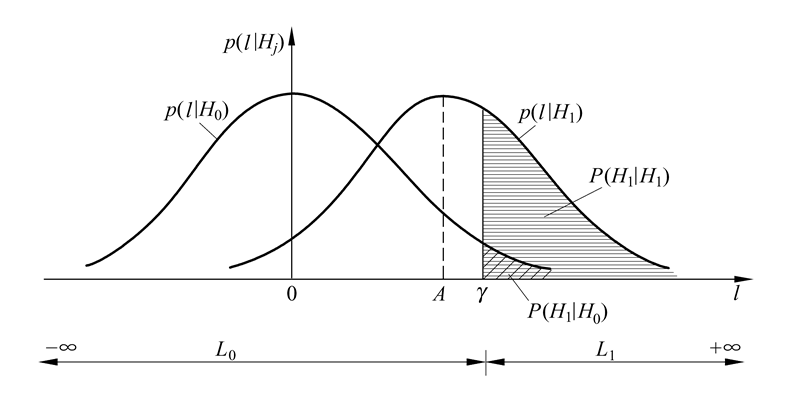
         图3.11判决概率P(H1|H0)和  P(H1|H1)示意图

     

利用参数η和d，把PD=P(H1|H1) 和PF=P(H1|H0)联系起来用图形表示，得到PD~PF曲线，即为接收机工作特性曲线(ROC)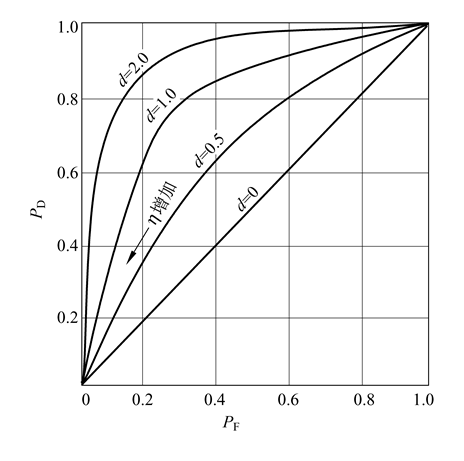                              













              图3.12接收机工作特性（ROC）


常把PD~PF曲线改为PD~d曲线，而以PF作参变量，即为检测特性曲线（检测概率与信噪比的关系曲线）。

                            










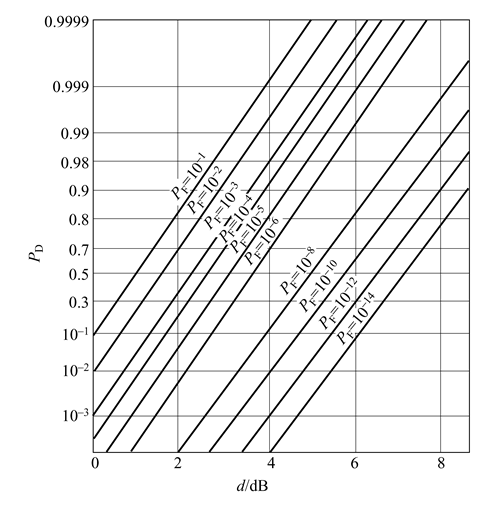
       图3.13检测概率PD与信噪比d的关系


如果λ(x)是 x 的连续函数，则接收机工作特性有共同特点。

（1）所有连续似然比检验的接收机工作特性都是上凸的。

（2）所有连续似然比检验的接收机工作特性均位于对角线PD=PF之上。

（3）接收机工作特性在某点处的斜率等于该点上PD和PF所要求的检测门限η .

检测系统接收机工作特性可用于各种准则的分析和计算。如图3.14所示。


                        










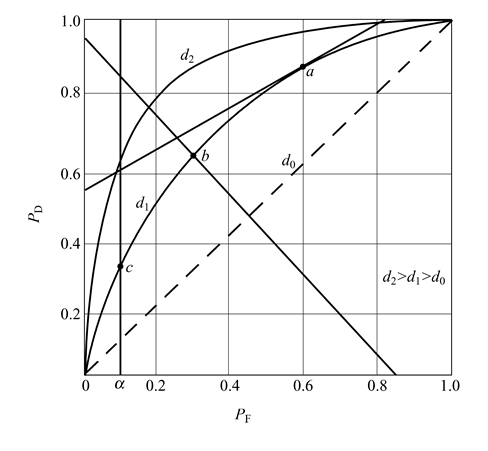
      图3.14接收机工作特性在不同准则下的解

所以说，检测系统接收机工作特性是似然比检验性能的完整描述.