1. 2 信号处理发展概况

一    发展历程

信号检测与估计理论是从40年代第二次世界大战中逐步形成和发展起来的。整个40年代是这个理论的初创和奠基时期。在这期间，美国科学家维纳(N．Wiener)和苏联科学家柯尔莫格洛夫(A．H. K)等作出了杰出的贡献。他们将随机过程和数理统计的观点引入到通信和控制系统来，揭示了信息传输和处理过程的统计本质，建立了最佳线性滤波理论，后人称之为维纳滤波理论。

诺思(D．O．North)于1943年提出了以输出最大信噪比为准则的匹配滤波器理论，随后在雷达和通信系统中获得了广泛的应用。1946年卡切尼科夫(B．A．K)提出了错误判决概率为最小的理想接收机理论，证明了理想接收机应在其输出端重现出后验概率为最大的信号，即是将最大后验概率准则作为一个最佳准则。1950年，当仙侬信息论刚问世不久，伍德沃(P．M．Woodward)就把信息量概念应用于雷达信号检测中来，提出了理想接收机应能从接收到的信号加噪声的混合波形中提取尽可能多的有用信息。为此，仅需知道后验概率分布，因此认为，理想接收机应是一个计算后验概率分布的装置。  

从1953年开始，人们直接利用统计推断中的判决和估计理论来研究雷达信号捡测和参量估计。在整个50年代，检测与估计理论发展迅猛。密德尔顿(D．Middleton)等人用贝叶斯准则(最小风险准则)来处理最佳接收问题，并使各种最佳准则统一于风险理论准则。这样，检测理论便发展到了成熟的阶段。1960年，同时有几部关于信号捡测与估计的著作问世，标志着经典捡测与估计理论已臻于完善。

六十年代初出现了卡尔曼(Kalman)滤波理论。60和70年代先后发展了非参量检测与估计理论，Robust检测与估计理论。Robust检测与估计的理论基础是休伯(P．J．Huber)于60年代中期提出的Robust统计学，70年代以后，被逐步应用到检测与估计领域，它适用于噪声统计特性部分确知的场合，目前这一理论尚处在开发研究阶段。

80年代以后，由于光纤通信、激光雷达及其它激光技术的发展，量子信道已日益重要，相应的量子检测与估计理论势必会接踵而上。1976年问世的赫尔斯特洛姆(C．W．Helstrom)的专著已为这一理论奠定了基石，但总的看来，量子检测与估计理论还处在初创时期，有一系列问题有待于研究和解决。

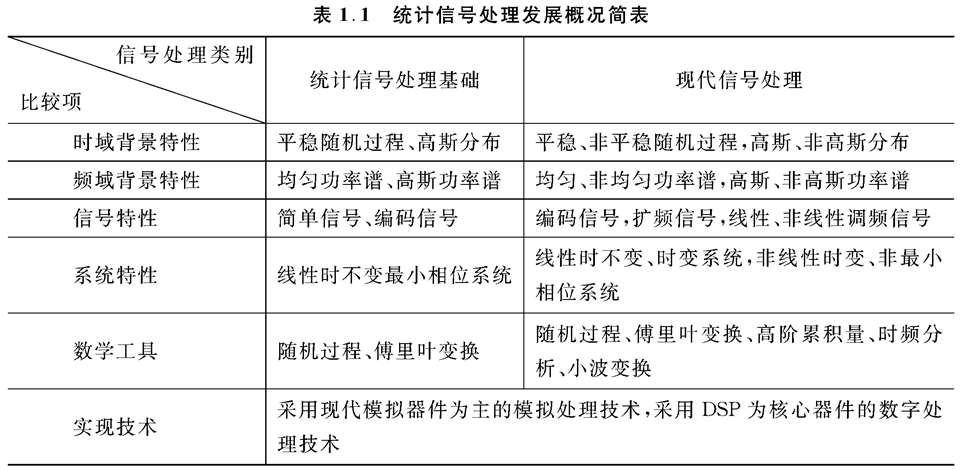
二    统计信号处理发展概况简表