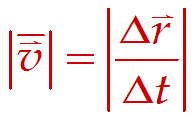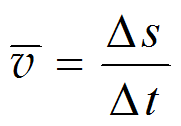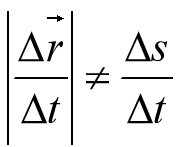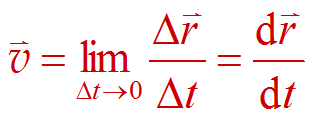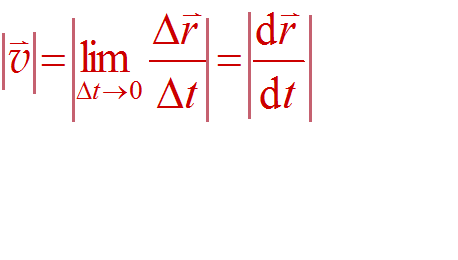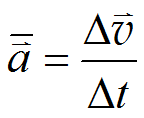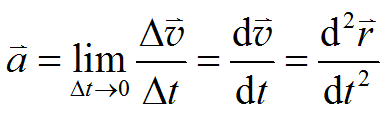位置矢量 位移 速度 加速度
-
1 位置矢量 运...
-
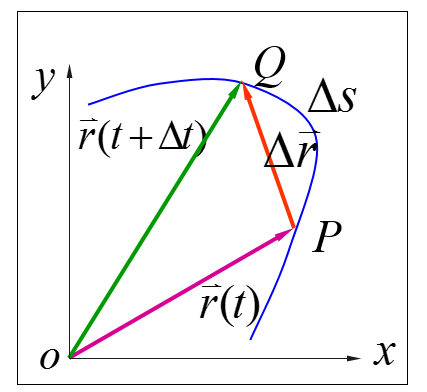
2 质点的位移 ...
上一节
下一节
一. 位置矢量(描述质点的位置)
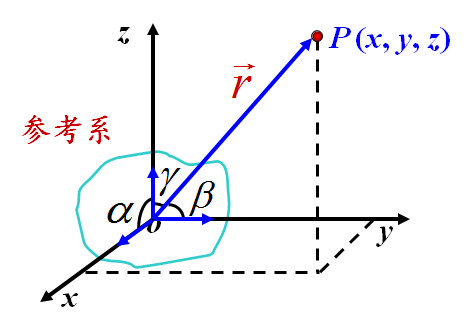
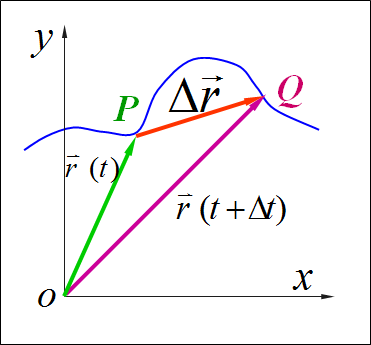
位置矢量:从坐标原点O到质点的位置P的有向线段,称为位置矢量,简称位矢。位矢可以用来确定质点相对于参考系的位置。
在三维直角坐标系中,也可以用P点的坐标(x,y,z)来表示质点的位置。而坐标x,y,z 分别是位矢沿三个坐标轴的投影
![]()
位矢的大小和方向余弦分别为
![]()
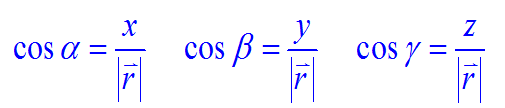
----------------------------------------------------------------------------------------------
*特别注意,位置矢量既有大小,也有方向,因此书写时其表达方式不要忘记矢量箭头
二. 运动学方程
当质点相对参考系运动时,用来确定质点位置的位矢和坐标x,y,z 都将随时间t变化,都是t的单值连续函数。表示运动过程的此函数式称为运动学方程,写作:
直角坐标(x,y,z)
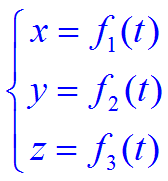
位置矢量
![]()
-----------------------------------------------------------------------------------------------------------
* 质点运动学的基本问题之一,是确定质点的运动学方程。为正确写出质点的运动学方程,先要选定参考系,坐标系,明确起始条件等,找出质点坐标随时间变化的函数关系。
轨道:质点在空间的运动路径称为轨道。
轨道方程:从运动学方程中消去时间t,即可得到轨道方程。