FIR滤波器的计算机辅助设计

求h(n)频响特性的函数freqz

格式：[H,w]=freqz(b,a,N)

lb,a--H(z)分子、分母多项式系数,对于FIR滤波器，b=h,a=1

lN--频率计算点数(N)

lH--对应数字频率w的频响特性

 通常w/pi（归一化）,则频率坐标以π为单位。

例

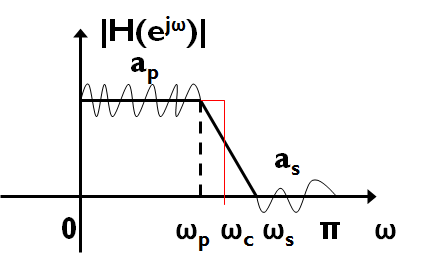
用Matlab设计FIR低通滤波器

技术指标：ωp=0.2π  ωs=0.3π

       ap=0.25dB  as=50dB

解：

分析步骤：

1.选择适当的窗函数

∵ as>50dB,∴选哈明窗

matlab：(hamming(N))’-- 产生N点哈明窗

tr=8π/N=ωs-ωp=0.3π-0.2π=0.1π

2.由tr确定滤波器长度

N=[8π/tr]  (朝+∞方向取整)  

Matlab:ceil(8*pi/tr)

3.确定理想低通滤波器参数

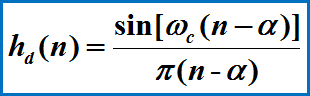
截止频率:ωc=(wp+ws)/2

取样时移:α=(N-1)/2

4.加窗处理(加哈明窗)

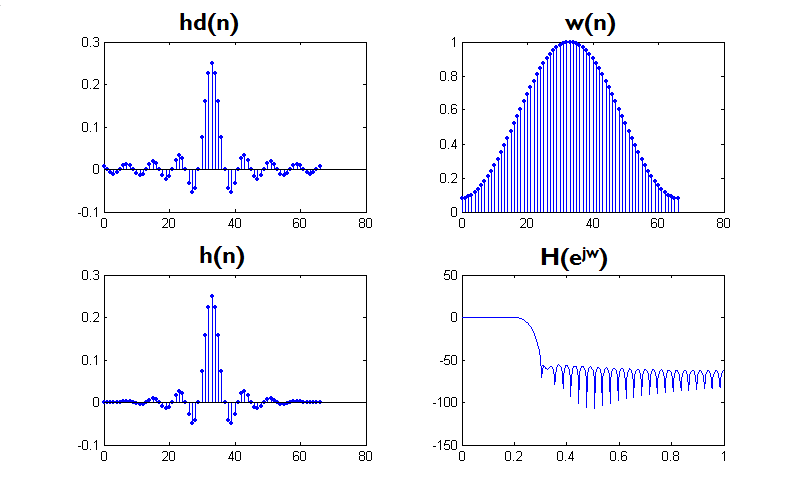
5.绘图[h(n),||等]

6.验证滤波器是否达到技术指标的要求

7.利用FIR低通滤波器进行滤波

%程序：FIRditong.m

wp=0.2*pi;ws=0.3*pi;

tr=ws-wp;

N=ceil(8*pi/tr)+1

n=[0:1:N-1];

wc=(ws+wp)/2;

m=n-(N-1)/2+eps;

hd=sin(wc*m)./(pi*m);%hd(n)

w_ham=(hamming(N))'; %哈明窗（N点）

h=hd.*w_ham;         %h(n)=hd(n)w_ham

[H,w]=freqz(h,[1],1000,'whole');%

mag=abs(H);          %幅频特性||

db=20*log10((mag+eps)/max(mag));

%||以dB为单位db=20lg|H|/|H|max

figure(1)%第一张图

subplot(221);stem(n,hd,‘.’);%画hd(n)

subplot(222);stem(n,w_ham,‘.’); %画哈明窗

subplot(223);stem(n,h,'.');%);%画h(n)

subplot(224);plot(w(1:501)/pi,db(1:501));

%画||（dB）(一半的频率点),频率轴以π为单位

%以下是技术指标的验算

delta_w=2*pi/1000;%Δw=2π/1000

ap=-(max(db(1:1:wp/delta_w+1)))

%验算通带最大波动（是否<0.25dB?)

as=-round(min(db(ws/delta_w+1:1:501)))

%验算阻带最小衰减（是否>50dB?)

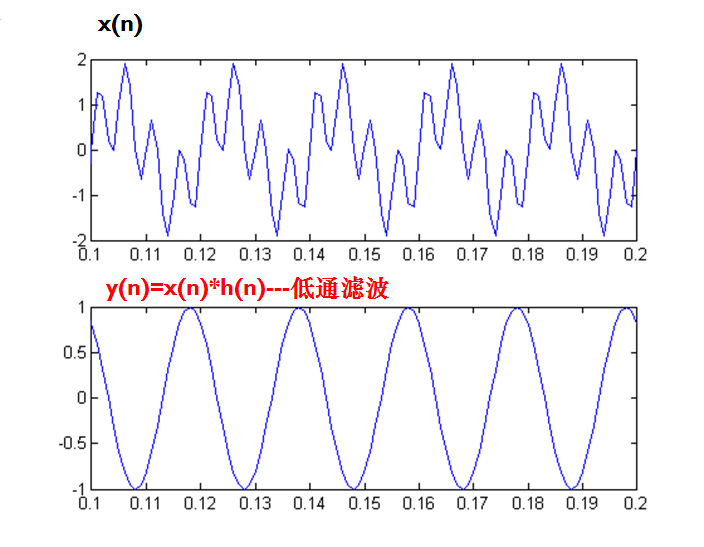
%应用FIR滤波器进行低通滤波(思考：哪一个信号可以通过？)

fs=1000;n2=1000;f1=50;f2=200;

j=0:1:n2-1;

x=sin(2*pi*f1*j/fs)+sin(2*pi*f2*j/fs);

%x(n)为50Hz和200Hz正弦波的迭加,数字频率

%ω1=2πf1/fs=0.1π, ω2=2πf2/fs=0.4π。

y=conv(x,h);%y=x(n)*h(n),低通滤波

t=j/fs;     %将时间轴改为连续时间t

figure(2)

subplot(211);plot(t,x);axis([0.1 0.2 -2 2])

            %画x

subplot(212);plot(t,y(1:n2));

axis([0.1 0.2 -1 1])

            %画滤波后的信号y

附

程序

FIRditong.m(下载附件 1.36 KB)