

(1)根据技术指标ωp ,ωs ,ap ,as计算巴特沃思滤波器的阶数N和3dB截止频率ωc。
[N,wc]=buttord(wp/pi,ws/pi,ap,as)
注:数字频率以π为单位。
(2)根据N,ωc确定数字滤波器H(z)分子/分母多项式的系数b,a。
低通滤波器:[b,a]=butter(N,wc)
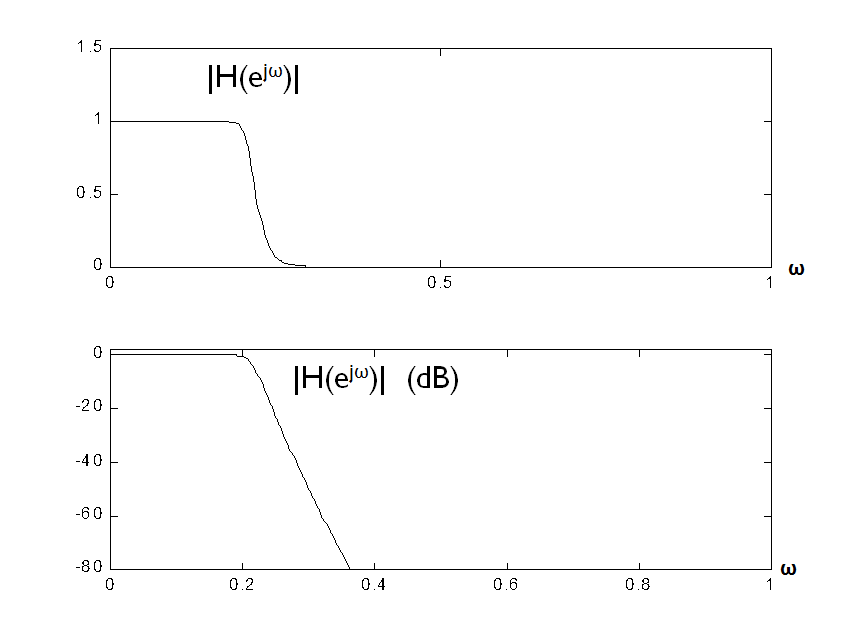
(3)画频响特性。
[H,w]=freqz(b,a,N1);
N1—做频响特性的点数。
wp=0.2π(rad),ws=0.3π(rad),
αp=1dB,αs=50dB
%程序:
wp=0.2*pi;ws=0.3*pi;
ap=1;as=50;%滤波器的技术指标
[N,wc]=buttord(wp/pi,ws/pi,ap,as);
%设计巴特沃斯模拟低通滤波器
[b,a]=butter(N,wc);%转换为数字低通
[H,w]=freqz(b,a,1000);
%求频响特性
mag=abs(H);
%幅频特性mag
db=20*log10((mag+eps)/max(mag));
%幅频特性db(以分贝为单位)
subplot(211);plot(w/pi,mag)
%绘出mag
subplot(212);plot(w/pi,db);
%绘出 db
设取样频率为fs1=1000Hz,用上述低通滤波器对音频信号:x(n)=x1(n)+x2(n)=sin(2π*50/fs1*n)+ sin(2π*200/fs1*n) (n=0,1,…999)进行滤波。
(1)编程绘出结果图形y(n)及其幅频谱|Y(f)|。
(2)x1(n)和x2(n),哪一个信号能够通过该滤波器?
*滤波语句:y=filter(b,a,x)
其中:x--输入信号x(n);
y--已滤波的输出信号y(n);
b,a--H(z)的分子/分母系数。
%程序:
fs1=1000;N=1000;
n=0:N-1;
x1=sin(2*pi*50/fs1*n); %x1(n)
x2=sin(2*pi*200/fs1*n); %x2(n)
x=x1+x2; %x(n)=x1(n)+x2(n)
X=fft(x,1024); %对x(n)做fft,得其频谱X(k)
y=filter(b,a,x); %对x(n)低通滤波,得滤波结果y(n)
Y=fft(y,1024); %对x(n)做fft,得其频谱X(k)
f=fs1/1024*(0:511); %将频率点k转换为实际频率f
figure(2)
subplot(221);plot(x);grid on;
%绘x(n)
subplot(222);plot(f,abs(X(1:512)));grid on;
%绘|X(f)|
subplot(223);plot(y);grid on;
%绘y(n)
subplot(224);plot(f,abs(Y(1:512)));grid on;
%绘|Y(f)|
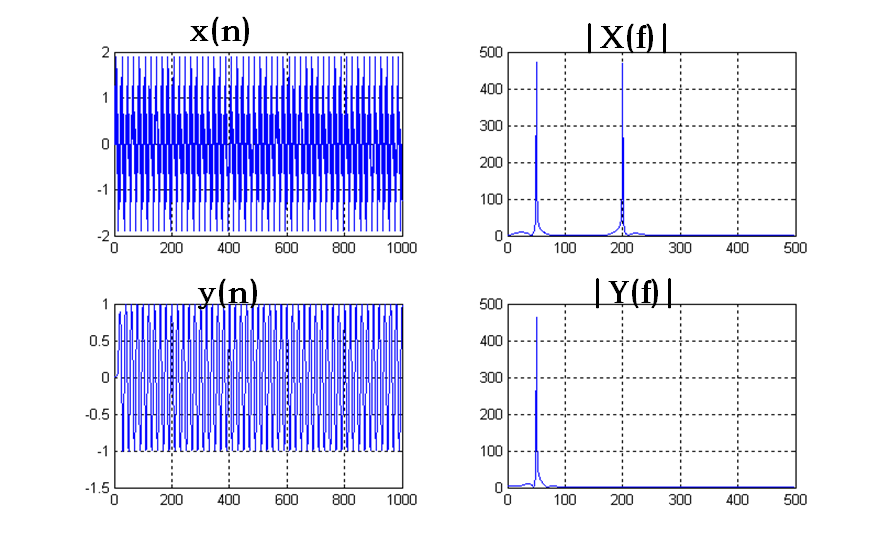
*只有x1(n)通过了该低通滤波器,x2(n)被滤除了。
附
声音和程序


