一、引言

直接用DFT做谱分析，其运算量有多大？

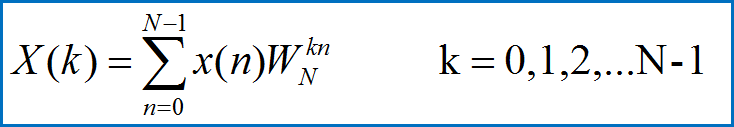
加快DFT运算速度---FFT(快速傅里叶变换）

二、时域抽取基2FFT算法

FFT的基本思想

l创始人：库利、图基（1965年）

l基本思想：将N点序列最终分成许多2点为一组的序列，分别计算它们的DFT；再将它们通过蝶形运算组合起来，算出整个序列的DFT。

旋转因子WN的性质

DIT-FFT基本原理 

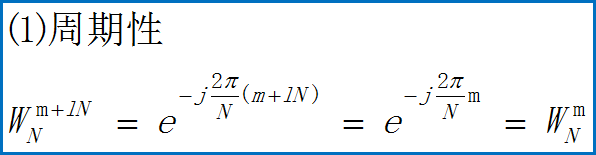
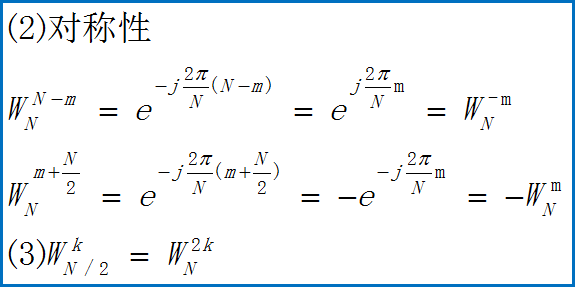
时域抽取法FFT(Decimation In Time FFT,简称DIT-FFT)。

设：x(n)的长度为N，且满足：

按n的奇偶，将x(n)分解为2个子序列：

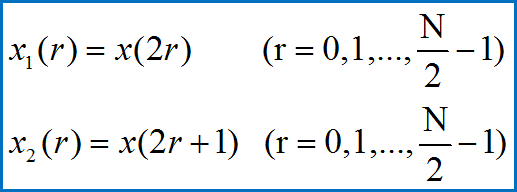
则x(n)的N点DFT为:

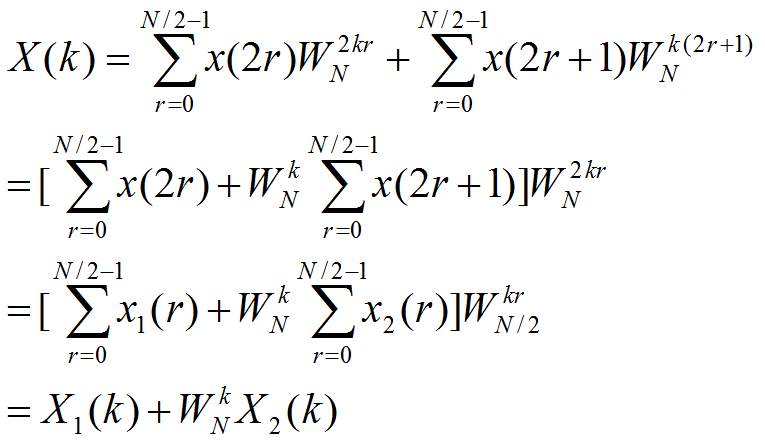
其中X1(k)和X2(k)分别为x1(r)和x2(r)的N/2点DFT，即: 

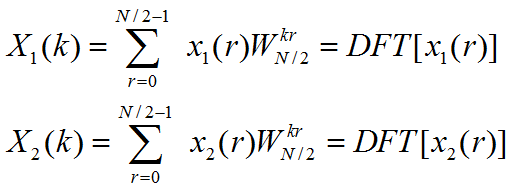
由于X1(k)和X2(k)均以N/2为周期，则X(k)又可表示为：

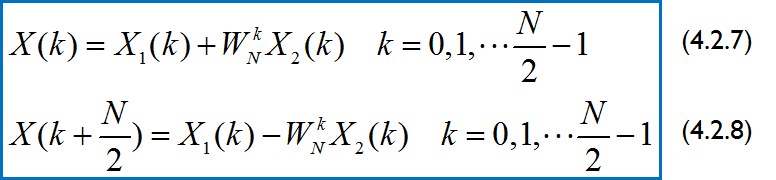
(4.2.7)和（4.2.8)可用蝶形运算表示。

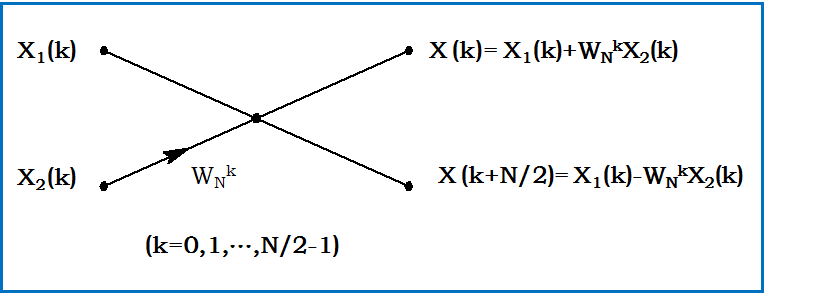
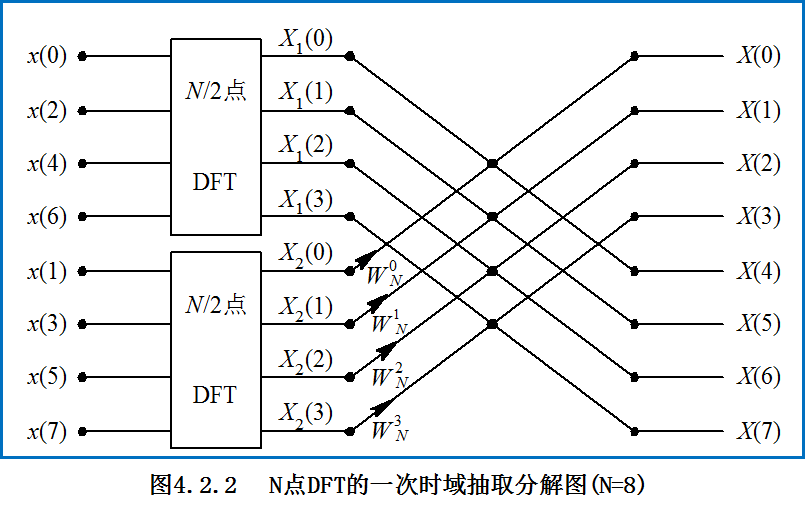
经过三次时域抽取分解，得整个 FFT运算流图：

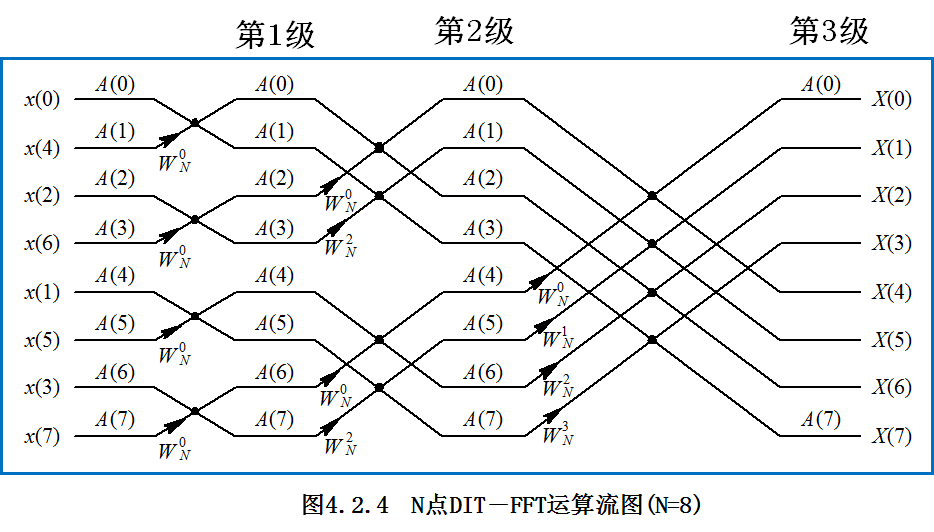
输入序列x(n)的倒序：

DIT―FFT算法的运算量

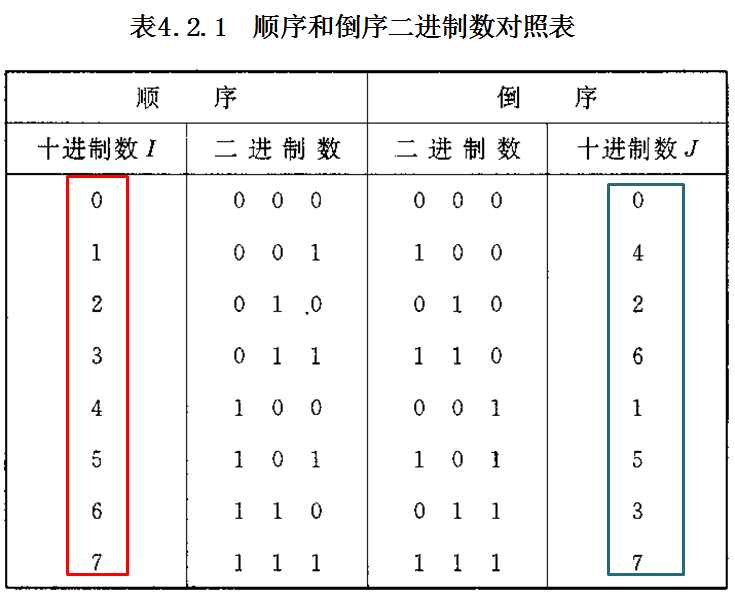
每个蝶形需1次复数乘法和2次复数加法，每级运算有N/2个蝶形故需N/2次复乘和N次复加。

M级运算共需要：

l例

对一幅N×N点的二维图像进行DFT,如用每秒可做10万次复数乘法的计算机，当N=1024时，需多长时间？

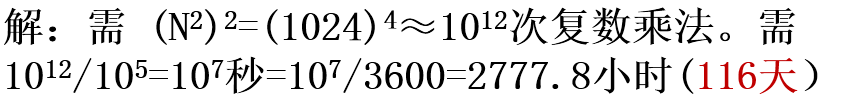
l例

对上述图像进行FFT（N=1024）,则需多长时间？

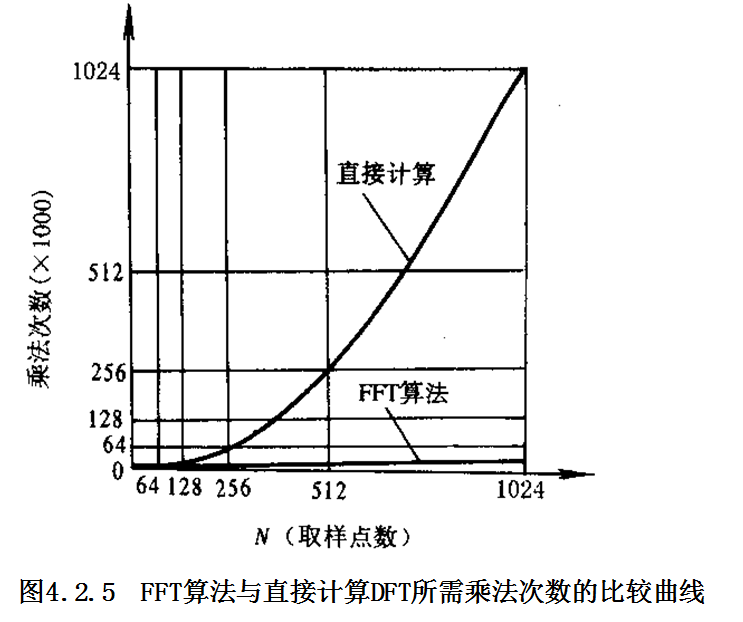
FFT算法的重大意义：

FFT算法使DFT运算时间大大缩短，从而使DFT运算得到广泛应用，也为数字信号处理技术应用于各种信号的实时处理创造了良好的条件，是数字信号处理学科诞生的里程碑。