信号的谱分析---计算并分析信号的DFT。

1.参数选择

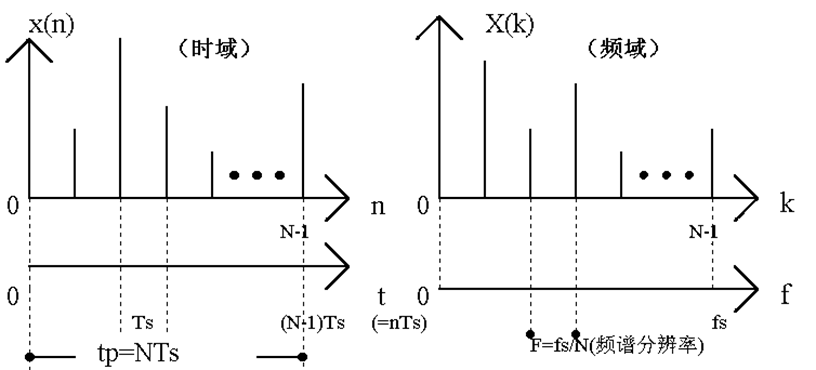
注：F越小，频谱分辨率越高。

各参数之间的关系

各参数必须满足

例

对实信号进行谱分析， 要求谱分辨率F≤10Hz，信号最高频率fc=2.5kHz，试确定：最小记录时间tPmin，最大的采样间隔Tsmax，最少的采样点数Nmin。

解：F=1/tp ≤10 ,  

即  tp≥1/F=1/10，   

故  tpmin=0.1s；

因  fs≥2fc=5kHz= fsmin， 

故  Tsmax=1/fsmin=1/5000s=0.2ms

   Nmin=2fc/F=5000/10=500点

2.用FFT计算频谱X(k)

设x(n)为长度N的实序列，则X(k)=FFT[x(n)]  (k=0,1,…,N-1)

Matlab语句：y=fft(x,N)

幅频谱

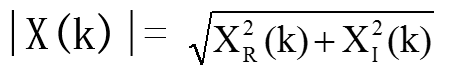
Matlab语句：abs(y)

相频谱

Matlab语句：angle(y)

功率谱

（突出主频率）

Matlab语句：PSD=y.*conj(y)/N

由于X(k)的对称性，所以幅频谱、相频谱及功率谱均画N/2点即可。

例

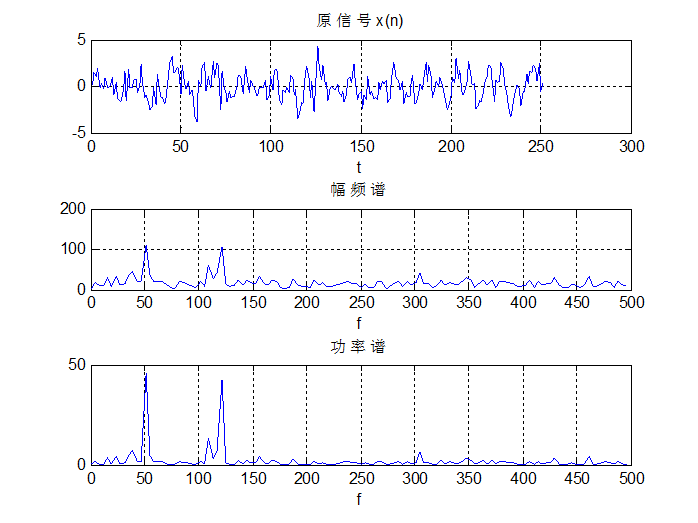
设信号为x(t)=sin(2πf1t)+sin(2πf2t)+随机噪声，f1=50Hz, f2=120Hz,以取样频率fs=1kHz对x(t)进行取样,样本长度tp=0.25s,得x(n),对x(n)作256点FFT,得频谱X(k)。

编程实现：画原信号x(n),幅频谱|X(k)|以及功率谱PSD(k),对信号进行谱分析。

%谱分析程序：

fs=1000;                  %采样频率

t=0:1/fs:0.25;              %时间范围          

N=256;                   % 做频谱分析点数N 

f1=50;f2=120; 

s=sin(2*pi*f1*t)+sin(2*pi*f2*t); %正弦信号    

x=s+randn(size(t));           %x(n)

Y=fft(x,N);                %对x(n)做N点fft

PSD=Y.*conj(Y)/N;            %功率谱           

f=fs/N*(0:N/2-1);            %频率轴   

subplot(311);plot(x);          %画x(n)  

subplot(312);plot(f,abs(Y(1:N/2)));  % 画幅频谱 

subplot(313);plot(f,PSD(1:N/2));    % 画功率谱                      

附

谱分析程序

pufenxi.m(下载附件 763 B)

3.读频谱图

l信号存在哪些频率分量，它们就是谱图中峰值对应的频率点。

l频谱图中，任意点k对应实际频率为f=kF=kfs/N   

l频率轴的5种定标方式

k--频率点      （最高：k=N/2-1点）

f--频率（Hz）（最高：f=fs/2）

Ω--角频率（rad/s）  Ω=2πf  (最高:Ω=Ωs/2)

ω--数字频率（rad） ω=2πf/fs (最高:ω=π)

f’=f/fs--归一化频率    （最高：f’=0.5）