一、DFT的定义

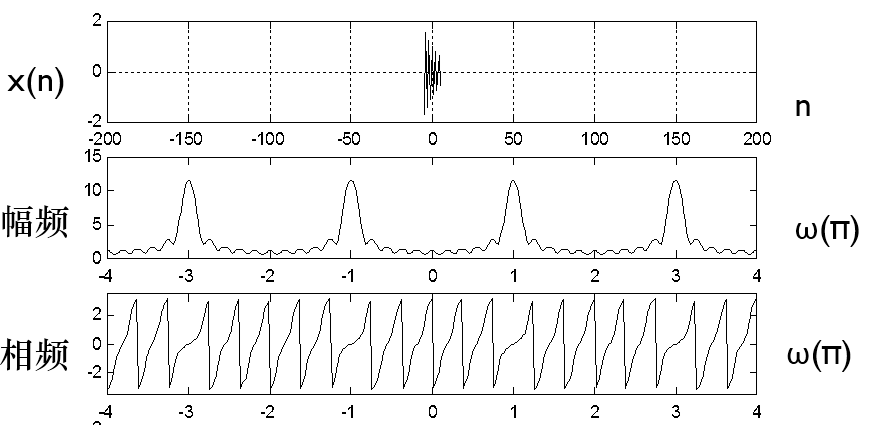
l引言

序列的傅里叶变换(FT)：    

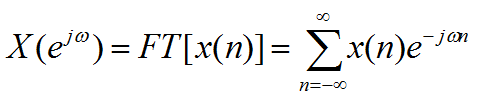
ω在0~2π(rad)内变化，仍是连续的,须经离散化才能在计算机上处理。

l方法

在单位圆上均匀取样，将0~2π等分为N点，第k点频率ωk=(2πk)/N,则:

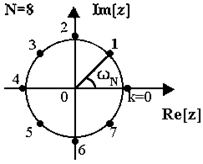
序列x(n)的DFT:

例1

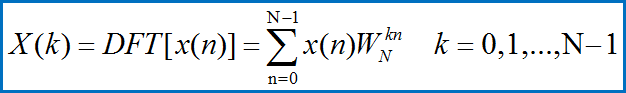
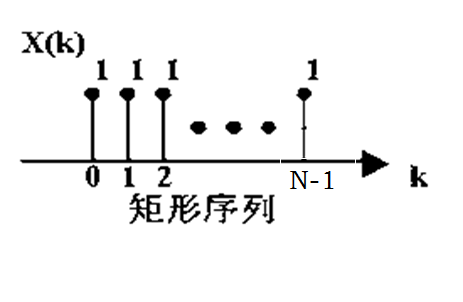
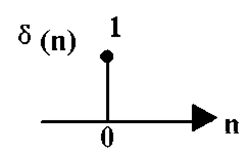
x(n)=δ(n)。 求：x(n)的N点DFT。

解：

 

例2

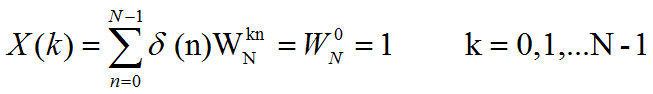
x(n)=R4(n) ，求x(n)的8点和16点DFT。

解：

设变换区间N=8，则：

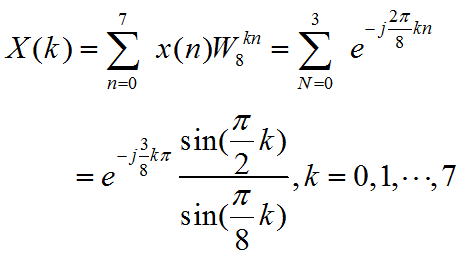
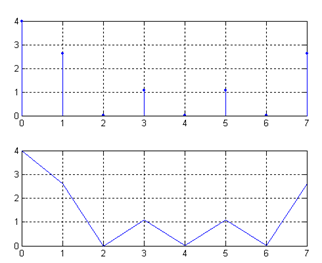
N=16：

二、DFT的计算机实现

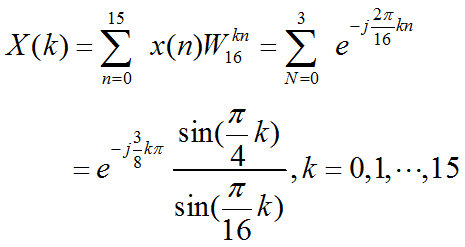
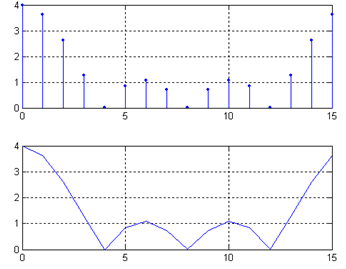
lDFT/IDFT公式的矩阵形式:

例3

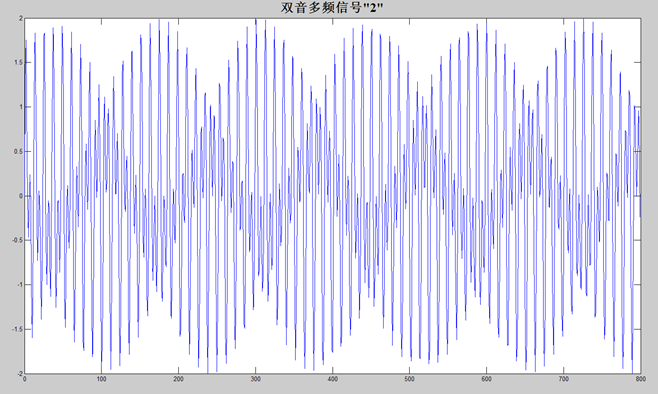
双音多频信号"2"表达式:

x(n)=sin(2πn*697/8000)+sin(2πn*1336/8000)，

编程绘出x(n)的幅频谱。(DFT的点数N=800)

%DFT程序

 N1=800;f1=697;f2=1336;

 fs=8000;n=0:N1-1

 xn=sin(2*pi*f1/fs*n)+sin(2*pi*f2/fs*n);

 %xn---双音多频信号“2”

 M=length(xn);                  %x(n)的长度M

 N=input('变换区间N='); %变换区间N

 xn=[xn zeros(1,N-M)];     %补0,使xn长度为N

 n=0:N-1;k=0:N-1;

 nk=n'*k;

 wn=exp(-j*2*pi/N);           %旋转因子矩阵WnK

 wnK=wn.^nk;

 xk=xn*wnK                %xk=DFT[xn]

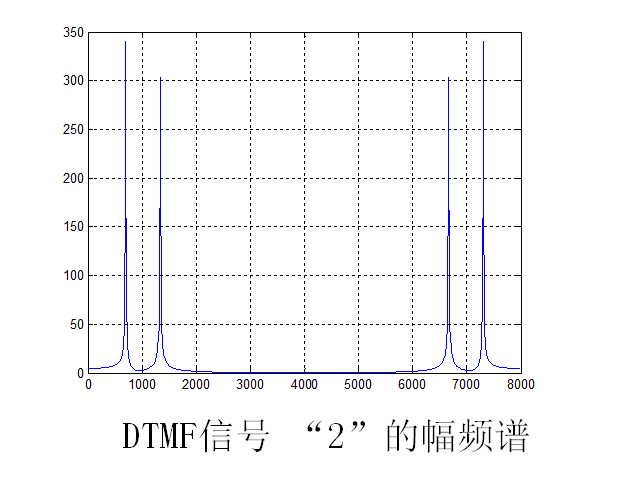
附

DFT程序

DFTchengxu.m(下载附件 679 B)

三、DFT隐含周期性

X(k+mN)=X(k)   (m为整数)

证：由于：

    (k,m,n均为整数) 

故：

例4

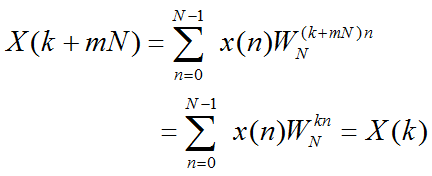
取：N=100,  k= -2N~2N, n= -2N~2N