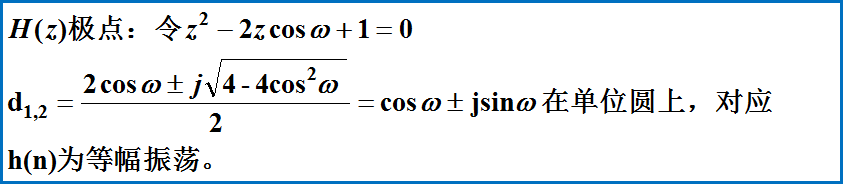1.传输函数与系统函数

设系统初始状态为零，h(n)=T[δ(n)]

h(n)----单位脉冲响应。

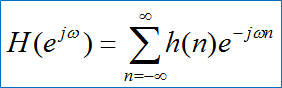
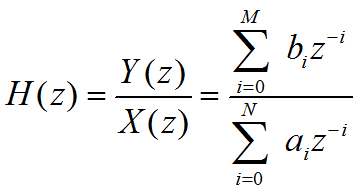
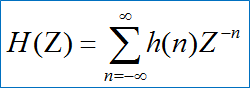
H(z)—系统函数。

利用Z变换分析频域特性：

若H(z)的收敛域包含单位圆|z|=1，则

例1

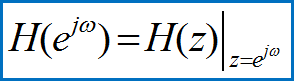
设一阶系统的差分方程为：

y(n)=by(n-1)+x(n)    (0<b<1)

例2

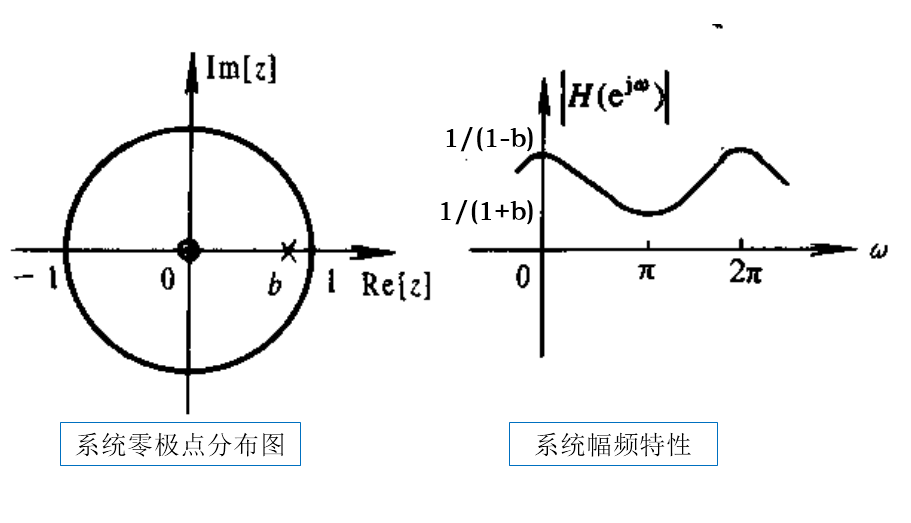
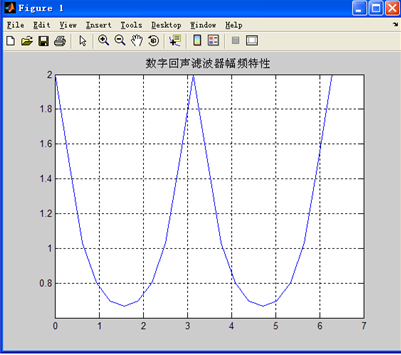
数字回声滤波器系统见下列差分方程：

y(n)=x(n)+αy(n-D)

其中：α--反射系数，表示声波经过反射后产生的衰减

  D--反射造成的延时

  x(n)--原声波信号

  y(n)--单反射回声信号

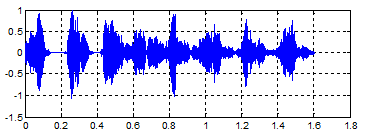
原始声音（鸟鸣） 

   

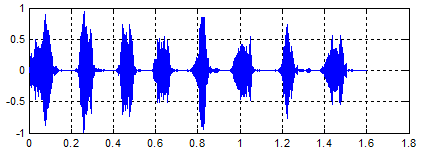
回声信号   

 

附

程序

shili1.m(下载附件 336 B)

2.用H(z)极点分析系统特性

lH(z)的零极点

(1)极点--使H(z)=∞的点，即：使H(z)分母多项式=0的点，符号：“×”
(2)零点--使H(z)=0的点，即：使H(z)分子多项式=0的点，符号：“○”

例1

lH(z)极点决定h(n)的形状

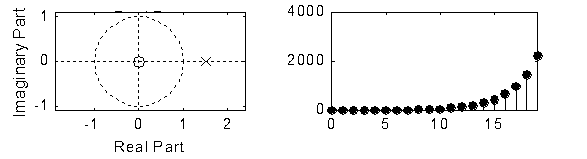
(1)H(z)实极点dj=a      

 h(n)     

|a|<1  衰减序列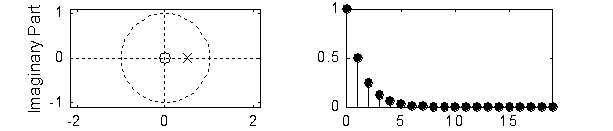  

|a|=1   等幅序列

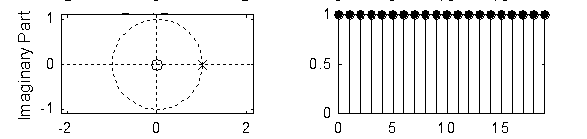
|a|>1   增幅序列

 

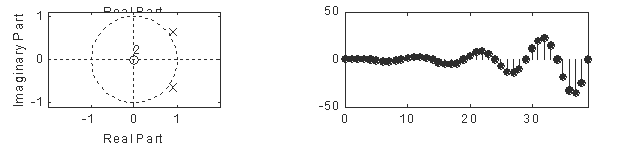
   h(n)  

 |a|<1   衰减振荡序列

 |a|=1   等幅振荡序列

 |a|>1   增幅振荡序列

例1

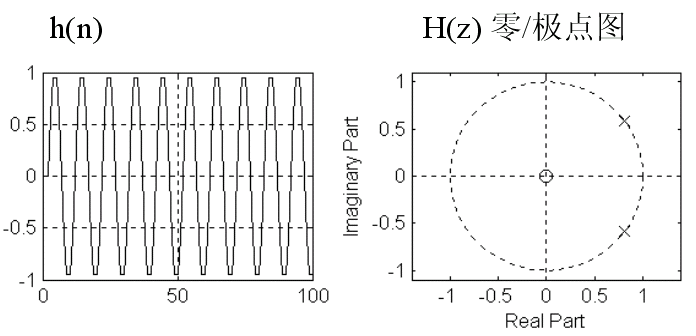
设计一个数字振荡器系统，指标：频率f0=1KHz,取样频率fs=10KHz。

求：

(1)该系统的单位脉冲响应h(n)

(2)系统函数H(z)的零极点分布图

解：

h(n)=sin(ωn)u(n)，为了利用DSP芯片等硬件实时产生h(n),必须找到h(n)满足的差分方程，用迭代法实现。

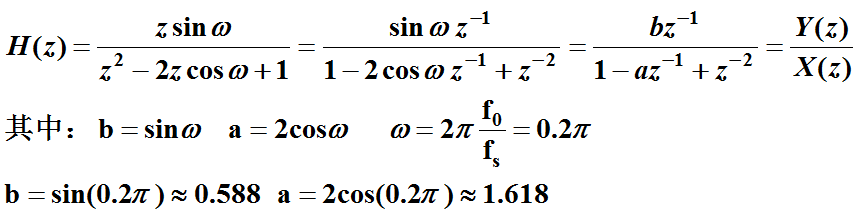
%  迭代法产生数字振荡器单位脉冲响应

clear

clc

b=0.588;a=1.618; %滤波系数

N=100;                 %h(n)的点数

b1=[0 b];

a1=[1 -a 1];

x=zeros(1,N);         %产生x(n)=δ(n)

x(1)=1;

h=filter(b1,a1,x);   %解差分方程，求h(n)

subplot(221);plot(h);

subplot(222);zplane(b1,a1);

附

程序

shili2.m(下载附件 188 B)