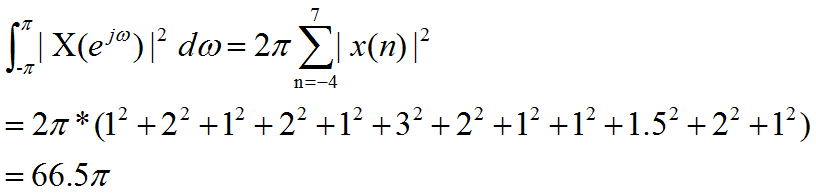1.序列的傅里叶变换

引言

频域分析---研究信号和系统的频率表示。

例

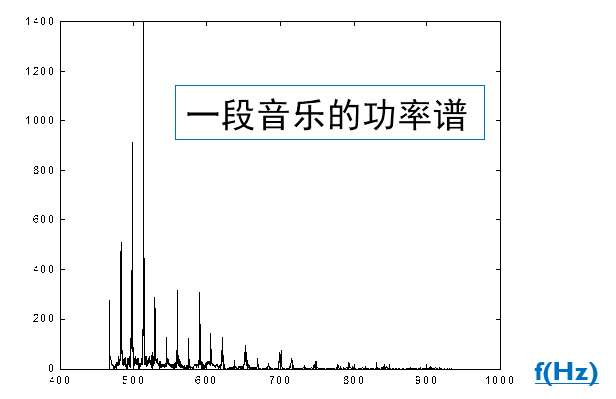
（1）听觉系统---声音的功率谱 

（2）三棱镜--频域分析仪

将白光分解为七种不同颜色（频率）的光

频谱分析的数学方法：傅里叶变换(FT)

序列的傅里叶变换(FT)

设：连续信号为x(t),则x(t)的傅里叶变换为：

FT成立的充要条件是x(n)绝对可和，即：

序列的傅里叶反变换：

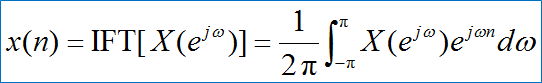
物理含义：任意工程信号可分解为无数个虚指数信号/2π之和，其系数即频谱X()。

例

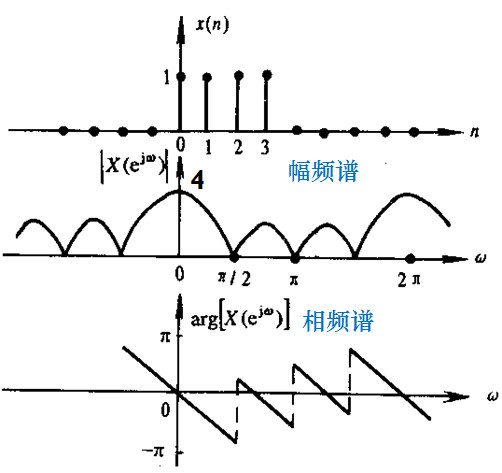
设x(n)=RN(n)， 求x(n)的FT

解：

 

R4(n)的幅频谱和相频谱

2.序列傅里叶变换的主要性质

FT的周期性

线性

时移与频移

时域卷积定理---时域卷积对应频域乘法

频域卷积定理---时域乘法对应频域卷积

帕斯维尔定理

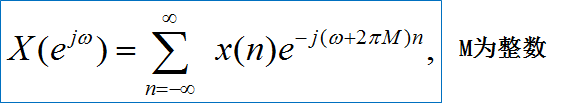
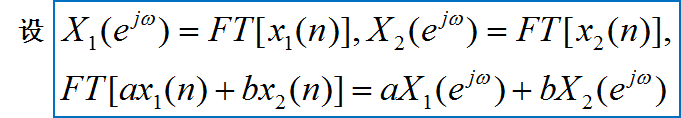
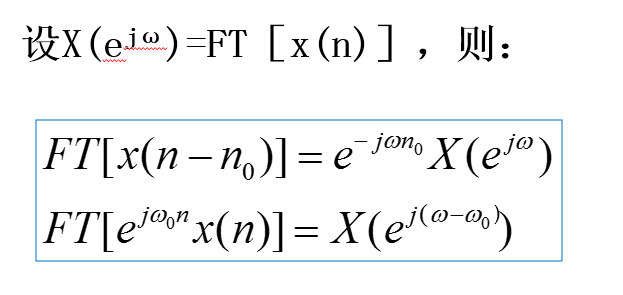
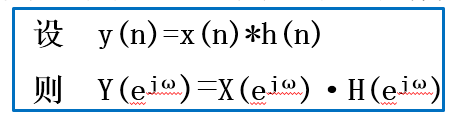
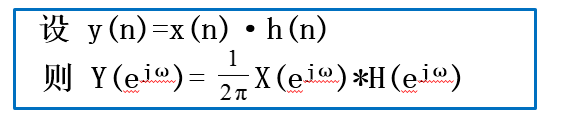
信号时域总能量=频域总能量

例

求：

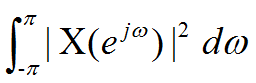
解：根据帕斯维尔定理得：