1.时域离散系统的N阶线性常系数差分方程

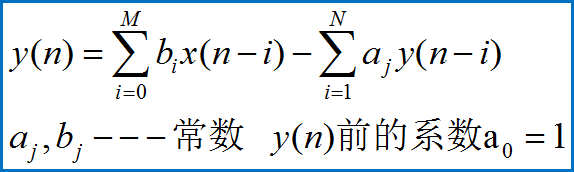
注：

差分方程的阶数=N1-N2  

N1--y(n-i)项最高序号；

N2--y(n-i)项最低序号。

N阶差分方程需N个初始条件：y(-1),y(-2),…,y(-n)

2.差分方程求解---递推法（迭代法）

例

设系统用差分方程y(n)=ay(n-1)+x(n)

描述，输入序列x(n)=δ(n)，求y(n) 

(1)设初始条件：y(-1)=0

解：

y(n)=ay(n-1)+x(n)

n=0时，y(0)= ay(-1)+δ(0)=1

n=1时，y(1)=ay(0)+δ(1)=a

n=2时，y(2)=ay(1)+δ(2)=

...

图形：(取a=1/2)

  (2)设初始条件：y(-1)=1

n=0时，y(0)=ay(-1)+δ(0)=1+a

n=1时，y(1)=ay(0)+δ(1)=(1+a)a

n=2时，y(2)=ay(1)+δ(2)=(1+a)

...

注：

（1）初始条件不同，y(n)不同。 

（2）差分方程本身不能确定系统的因果性，需用初始条件限制。

图形：(取a=1/2)

%求解差分方程程序：(注：Matlab下标从1开始)

clear                         %清除内存

clc                            %清屏

a=1/2;N=10;

x=zeros(1,N);x(1)=1;           %产生x(n)=δ(n)

yfu1=input('初始条件y(-1)=');%y(-1)

y(1)=a*yfu1+x(1);                %计算y(0)

for n=2:N

%解差分方程y(n)=ay(n-1)+x(n)(n=1:N-1)

y(n)=a*y(n-1)+x(n);

end

stem(0:N-1,y,‘b’);grid on;           %绘图

附

求解差分方程程序

shili4.m(下载附件 367 B)

*差分方程应用举例：银行还贷问题

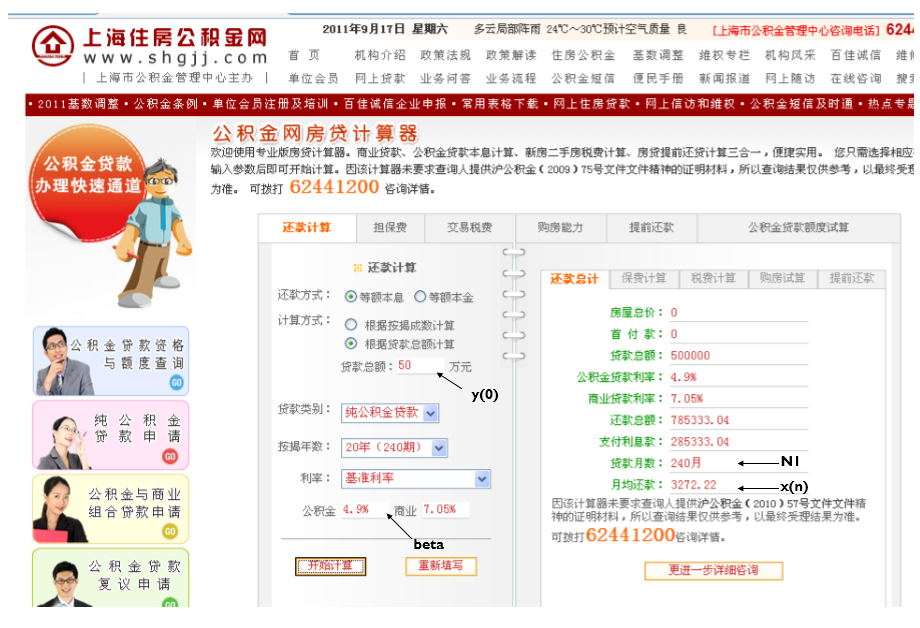
设采用公积金贷款50万元,利率beta=4.9%,

月还款额为固定值（等额本息）。

则该问题的差分方程如下:

y(n)=(1+beta/12)y(n-1)-x(n) (n=1,2,……)

x(n)--月还款额；beta--年利率；

y(n-1)--上月剩下的贷款总额；

beta/12*y(n-1)--贷款在第n个月的利息;

y(n)--第n个月后剩下的贷款总额。

本例：y(0)=50(贷款总额), beta=0.049,

    x(n)=0.32722

求：经过多少年能还清贷款？

%程序:

clear

clc

y(1)=50;

N=300;   

beta=0.049;

x=0.327222;

for n=2:N

  y(n)=(1+beta/12)*y(n-1)-x

      if  y(n)<=1e-3

          N1=n;

         break;end

     end

N1=N1

运行结果：N1=241,y(N1)=0

（20年后还清贷款）

附

程序

shili5.m(下载附件 182 B)