1.加法和乘法

相同序号的序列值对应相乘和相加。

例1

x1(n)={1,1,1},x2(n)={1, 2, 3}

                  ↑n=0

求：

(1) y1(n)=x1(n)+x2(n)

(2) y2(n) =x1(n)x2(n)

解:

(1)y1(n)={1,3,4,1}

       ↑

(2)y2(n)={2,3}

2.移位

x(n-n0)--x(n)右移n0位，称为x(n)的延迟序列。

x(n+n0)--x(n)左移n0位，称为x(n)的超前序列。

例2

x(n)={1,2,3} ,求：x(n-1)和x(n+1)

解：

x(n-1)={0,1,2,3}

x(n+1)={1,2,3}

      ↑

3.翻转：x(-n)

以n=0为轴，将x(n)图形对该轴翻转。

例3

x(n)={1,2,3},求：x(-n)

解：x(-n)={3,2,1}

          ↑

4.尺度变换（令m为整数，且m>1)

1.x(mn)--m抽取，即每隔m点抽取1点。对应时间轴压缩到原来的1/m。

2.x(n/m)--m插值，即每2点插入m-1个0。对应时间轴扩展到原来的m倍。

例4

x(n)={3,2,1,-1}，求x(2n),x(1/2n)

解：

x(2n)={3,1}；

x(1/2n)={3,0,2,0,1,0,-1}

*综合运算

例5

5.卷积运算

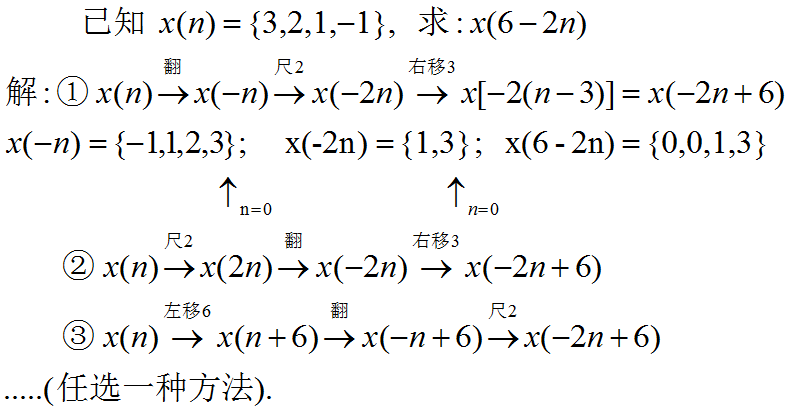
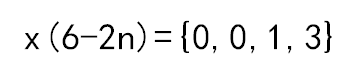
y(n)=x(n)* h(n)                   

“*”:卷积，即y(n)=  

运算方法

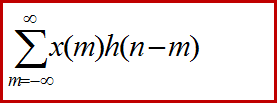
1.直接法

①将x(n)和h(n)用x(m)和h(m)表示；

 将h(m)翻转，得h(-m)；

 将h(-m)右移n，得h(n-m)。

②确定m的范围。

③将x(m)和h(n-m)相同m的序列值对应相乘，再相加。

例：

设x(n)=R4(n)，h(n)=R4(n)

求：y(n)=x(n)*h(n)。

解：

  

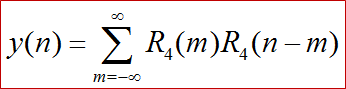
R4(m)的非零值区间为：0≤m≤3

R4(n-m)的非零值区间为：0≤n-m≤3

其乘积值的非零区间，要求：0≤m≤3，n-3≤m≤n 

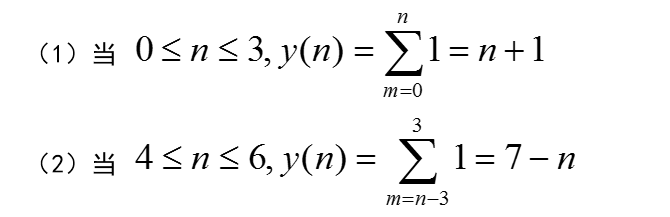
则：

*注:

y(n)的长度：Ny= Nx+Nh-1

其中：Nx--x(n)的长度；

    Nh--h(n)的长度。

2.列表法（适用于求有限长序列的卷积）

运算步骤：

（1）列表：第1行和第2行是x1(n)及其序号，

     第1列和第2列是x2(n)及其序号；

（2）填元素：填对应行列所在项的乘积；

（3）斜线上元素求和；

（4）定序号：各序号=对应行序号+列序号。

例6

x1(n) ={1,1,1},x2(n)={1,2} 

采用列表法求：y(n)= x1(n)*x2(n) 

%本例的matlab程序

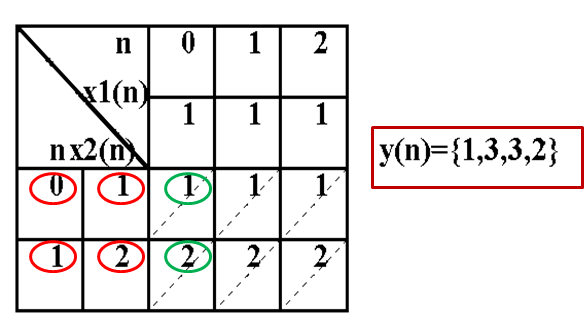
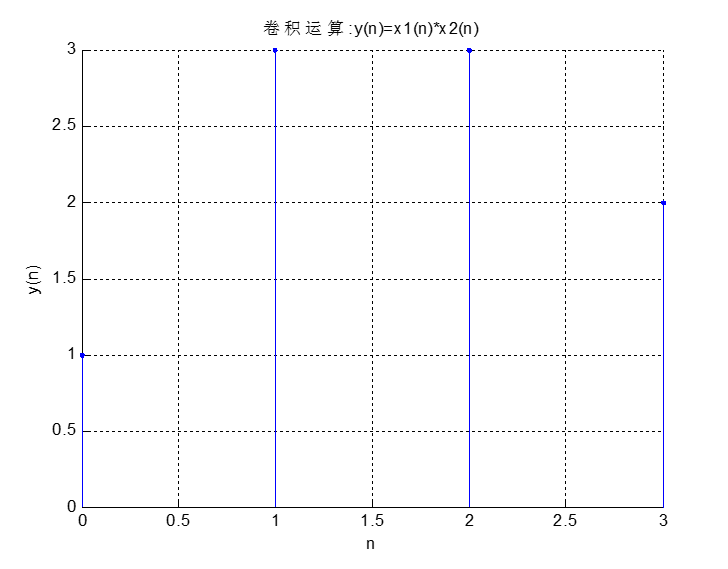
附

卷积运算程序：

shili3.m(下载附件 263 B)