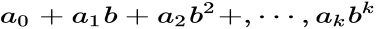什么是二进制

计数系统

人们在生产实践和日常生活中，创造了多种表示数的方法，这些数的表示规则称为数制。例如，人们常用的十进制，钟表计时中使用的1h等于60min、1min等于60s的六十进制，我国曾使用过1市斤等于16两的十六进制，计算机中使用的二进制，等等。

进制

在基数b的位置记数系统(其中b是一个正自然数，叫做基数)，b个基本符号(或者叫数字)对应于包括0的最小b个自然数。 要产生其他的数，符号在数中的位置要被用到。最后一位的符号用它本身的值，向左一位其值乘以b。一般来讲，若b是基底，我们在b进制系统中的数表示为

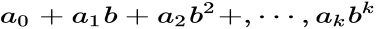
的形式，并按次序写下数字a₀a₁a₂a₃...a_k。这些数字是0到b-1的自然数

一般来讲，b进制系统中的数有如下形式：

1.十进制数

十进制的基数为10，即“逢十进一”。它含有l0个数字符号：0、1、2、3、4、5、6、7、8、9

2.二进制计数

17世纪至18世纪的德国数学家莱布尼茨，是世界上第一个提出二进制记数法的人。用二进制记数，只用0和1两个符号，无需其他符号 。

二进制数据也是采用位置计数法，其位权是以2为底的幂。例如二进制数据110.11，逢2进1，其权的大小顺序为2²、2¹、2º、
   二进制的基数为2，即“逢二进一”。它含有2个数字符号：0和1。
二进制是计算机中采用的数制，所有的数据信息在计算机内部都是以二进制形式来表示和处理的。为什么计算机会采用二进制数呢?这是因为二进制数具有如下特点。

1）可行性。二进制只有两个数字，在物理上只需要两种状态来表示，这在电路上是很容易实现的，如晶体管的导通和截止，开关的开与合，电平的高与低。

2）简易性。二进制数的运算法则比较简单。例如，二进制数的加法法则如下。
0+0=0   0+1=1+0=1  1+1=10 （逢二进一） 简单的运算法则使得电路实现起来比较简单。
【例】：将二进制数据111.01写成加权系数的形式。
解：

二进制和十六进制，八进制一样，都以二的幂来进位的

3.八进制

八进制的基数为8，即“逢八进一”。它含有8个数字符号：0、1、2、3、4、5、6、7。

4.十六进制

十六进制的基数为16，即“逢十六进一”。它含有16个数字符号：0、1、2、3、4、5、6、7、8、9、 A B、C、D、E、F分别表示十进制数10、11、12、13、14、15。

应当指出的是，二进制、八进制、十六进制和十进制都是计算机中常用的数制。既然存在不同的数制，那么在给出一个数时必须指明该数是什么数制中的数。例如，（1001)₁₀、(1001)2、(1001)8、（1001)16分别表示十进制、二进制、八进制、十六进制中的数1001，但它们的数值是不同的。还可以用后缀字母表示不同数制中的数。例如，1001D、1001B、1001Q、1001H也可以分别表示十进制、二进制、八进制、十六进制中的数1001。

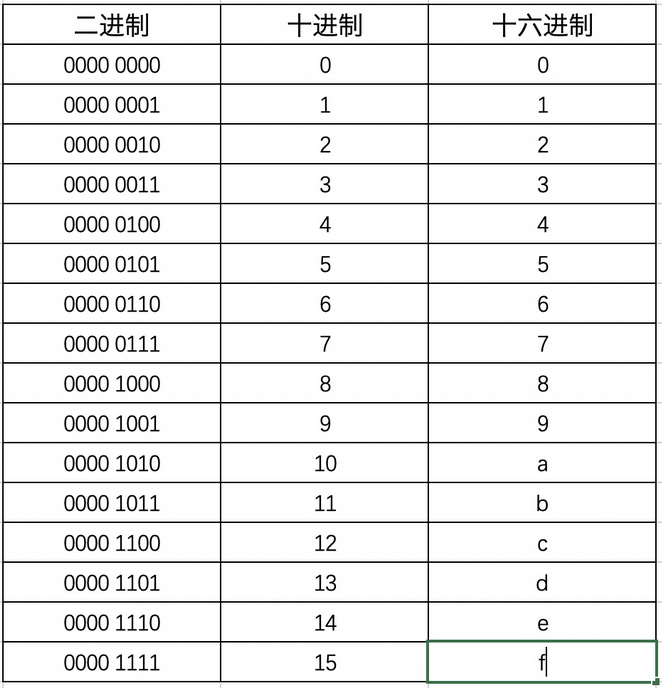
二进制数、十进制数、十六进制数

二进制运算

加法

二进制加法有四种情况： 0+0=0，0+1=1，1+0=1，1+1=10  (0 进位为1)

乘法

二进制乘法有四种情况： 0×0=0，1×0=0，0×1=0，1×1=1

减法

二进制减法有四种情况：0－0=0，1－0=1，1－1=0，0－1=1

除法

二进制除法有两种情况(除数只能为1)：0÷1=0，1÷1=1

实例

两个二进制数1001与0101的算数运算可表示为：

十进制转换二进制数

进制转换

二进制转换为十进制

方法：“按权展开求和”，该方法的具体步骤是先将二进制的数写成加权系数展开式，而后根据十进制的加法规则进行求和。

【例】：

规律：个位上的数字的次数是0，十位上的数字的次数是1，......，依次递增，而小数部分十分位的数字的次数是-1，百分位上数字的次数是-2，......，依次递减。

十进制转换为二进制

一个十进制数转换为二进制数要分整数部分和小数部分分别转换，最后再组合到一起。整数部分采用 "除2取余，逆序排列"法。具体做法是：用2整除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行，直到商为小于1时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来 例：125。

整数部分

小数部分要使用“乘 2 取整法”。即用十进制的小数乘以 2 并取走结果的整数(必是 0 或 1)，然后再用剩下的小数重复刚才的步骤，直到剩余的小数为 0 时停止，最后将每次得到的整数部分按先后顺序从左到右排列即得到所对应二进制小数。例如，将十进制小数 0.8125 转换成二进制小数过程如下 :

电路表示二进制数

2.各种数制间的转换

对于各种数制间的转换，重点要求掌握二进制整数与十进制整数之间的转换。

1.非十进制数转换成十进制数

将非十进制数转换成十进制数的方法很简单，即把各个非十进制的数按该数的基数（权）展开即可。

(1011.101)2=1×2³+0×2²+1×2¹+1×2⁰+1×2^-1+0×2^-2+1×2^-3

=8+0+2+1+0.5+0+0.125=(11.625)₁₀

(2)八进制数转换成十进制数

(345.67)₈=3×8²+4×8¹+5×8⁰+6×8^-1+7×8^-2=(229.859375)₁₀

(3)十六进制数转换成十进制数

(ABC.2F)₁₆=10×16²+11×16¹+12×16⁰+2×16^-1+15×16^-2

=(2748.18359375)₁₀

2.十进制数转换成其他进制数

（1)二进制数转换成十进制数

十进制数转换成其他进制数时，方法不止一种，但通常采用的方法如下：将其整数部分除以基数（权）取余数，将其小数部分乘以基数（权）取整数。

（1)十进制数转换成二进制数 不尘

十进制数转换成二进制数时，对其整数部分采用“除二取余”法，小数部分采用“乘二取整”法。

例如，将(215.6875)10转换成二进制数。对其整数部分除二取余，则得

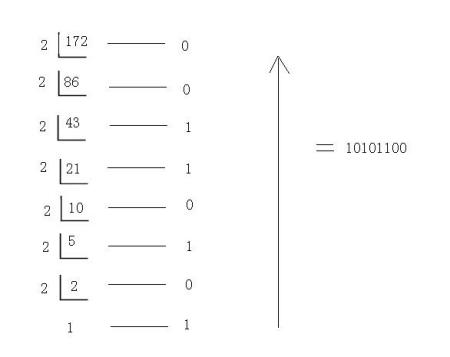
最后一个余数作为二进制数的首位，第一个余数作为二进制数的最低位。

对其小数部分乘二取整，则得

(0.6875)10=(0.1011)2

将整数和小数部分综合起来：(0.3125)₁₀=(0.0101)₂。

（2)十进制数转换成八进制数

将十进制数转换成八进制数时，对其整数部分采用“除八取余”，小数部分采用“乘八取整”，具体步骤参考十进制数转换成二进制数。

(3)十进制数转换成十六进制数

将十进制数转换成十六进制数时，对其整数部分采用“除十六取余”，小数部分采用“乘十六取整”且体步骤参考十进制数转换成二进制数。

3.非十进制数之间的转换

（1）二进制数与八进制数之间的转换

每1位八进制数最大是（7）10，相当于3位二进制数，即(7)10=(111)2，这就是说八进制1位对应于二进制3位。八进制数转换成二进制数的法则是“1位拆3位”，即把1位八进制数写成对应的3位二进制数，然后按权连接。

例如，将（2754.41)3转换成二进制数，可按“1位拆3位”的方法，即

所以，(2754.41)₈=(10111101100.100001)₂。

反之，二进制数转换成八进制数的法则是“3位并1位”，即以小数点为基准，整数部分从右至左每3位一组，最高位不足3位时在前面添0以补足3位；小数部分从左至右每3位一组，最低位不足3位时在后面添0补足3位，然后将各组的3位二进制数按2³、2¹、2⁰权展开后相加，得到一位八进制数。

例如，将（1010111011.0010111)₂转换为八进制数，可按“3位并1位”方法，即

所以，(1010111011.0010111)₂=(1273.134)₈。

(2）二进制数与十六进制数之间的转换

每1位十六进制数最大是（15）10，相当于4位二进制数，即（15）10=（1111）2，这就是说

十六进制1位对应于二进制4位。十六进制数转换成二进制数的法则是“1位拆4位”，即

把1位十六进制数写成对应的4位二进制数，然后按权连接。

例如，将（5A0B.1E)₁₆转换成二进制数，可按“1位拆4位”的方法，即

所以，(5A0B.1E)16=(101101000001011.0001111)2。

反之，二进制数转换成十六进制数的法则是“4位并1位”，即以小数点为基准，整数部分从右至左每4位一组，不足4位时在前面添0补足4位；小数部分从左至右每4位一组，最低位不足4位时在后面添0补足4位，然后将各组的4位二进制数按2³、2²、2¹、2⁰权展开相加，得到一位十六进制数。

例如，将（1110100101.01101011)₂转换成十六进制数，可按“4位并1位”的方法，即

所以，(1110100101.01101011)₂=(3A5.6B)₁₆

（3）八进制数与十六进制数之间的转换

这两种数制之间的转换可以用二进制数或十进制数作为中间过渡。例如，以十进制数作为中间过度，先将八进制数转换成十六进制数了，再将十进制数转换成十六进制数，这样就将八进制数转换成十六进制数了；反之，十六进制数转换成八进制数也是这样。

数制的概念

各种数制之间的转换

二进制（binary）是在数学和数字电路中指以2为基数的记数系统，是以2为基数代表系统的二进位制。这一系统中，通常用两个不同的符号0（代表零）和1（代表一）来表示  。数字电子电路中，逻辑门的实现直接应用了二进制，因此现代的计算机和依赖计算机的设备里都用到二进制。每个数字称为一个比特（Bit，Binary digit的缩写）

容易表示

二进制数只有“0”和“1”两个基本符号，易于用两种对立的物理状态表示。例如，可用"1"表示电灯开关的“闭合”状态，用“0”表示“断开”状态；晶体管的导通表示“1”， 截止表示“0”；电容器的充电和放电、电脉冲的有和无、脉冲极性的正与负、电位的高与低等一切有两种对立稳定状态的器件都可以表示二进制的“0”和“1”。而十进制数有10个基本符号（0、1、2、3、4、5、6、7、8、9），要用10种状态才能表示，要用电子器件实现起来是很困难的。

运算简单

二进制数的算术运算特别简单，加法和乘法仅各有3条运算规则（ 0+0=0，0+1=1，1+1=10和0×0=0，0×1=0，1×1=1 ），运算时不易出错。[其实计算机处理算术运算时都是加法和移位，并没有乘除法，如11B左移一位就成了110B,11B是十进制的3，而110B是6，看看是不是等于乘二，左移乘，右移就除，此外，二进制数的“1”和“0”正好可与逻辑值“真”和“假”相对应，这样就为计算机进行逻辑运算提供了方便。算术运算和逻辑运算是计算机的基本运算，采用二进制可以简单方便地进行这两类运算。