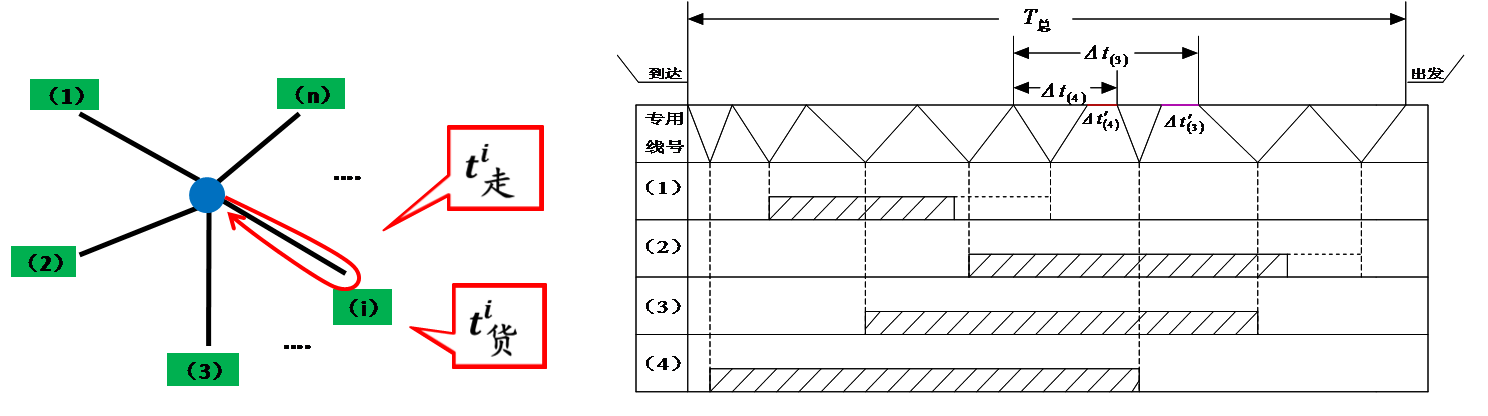
以装车站为背景,车流整列到发、一台机车作业条件下的放射形专用线取送顺序问题。其作业方法为：

空车整列到达车站，在到发线上进行必要的到达作业后，机车将空车分别送往各条专用线装车，装完的重车由该机车先后取回站内，编组成列出发。

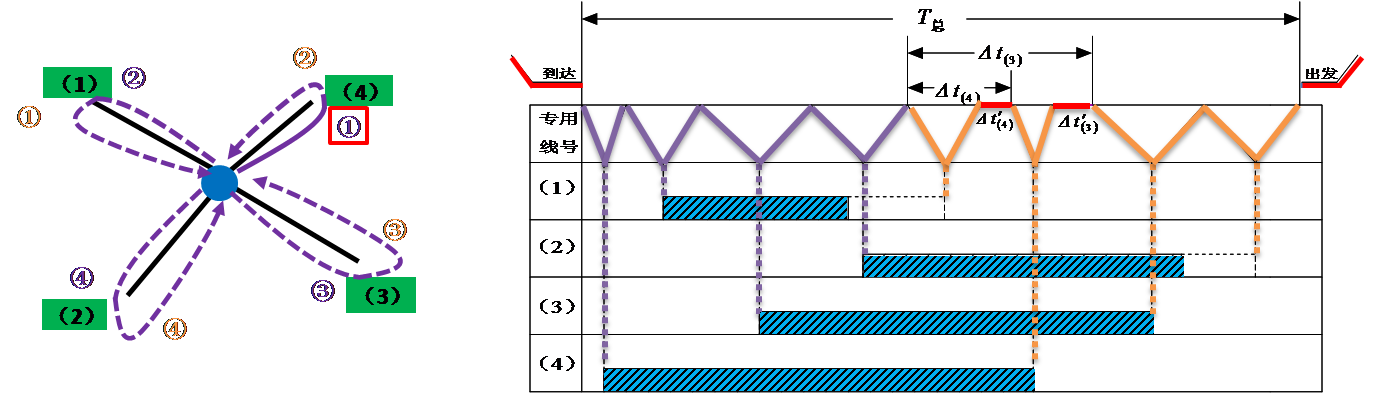
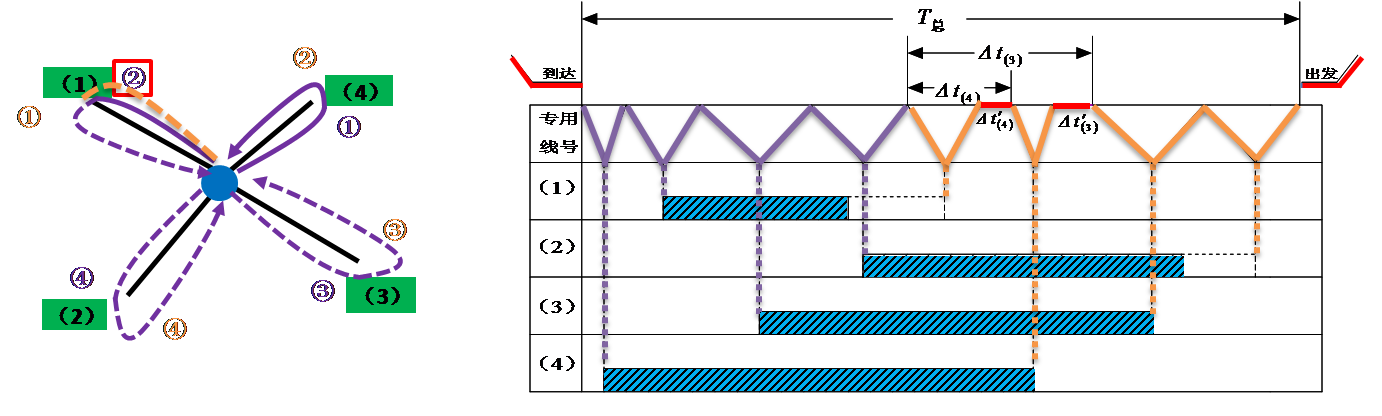
车辆在站总停留车小时的长短主要取决于从第一批车辆送车开始至全部车辆取回为止的时间，称之为技术作业总时间，记作T总。

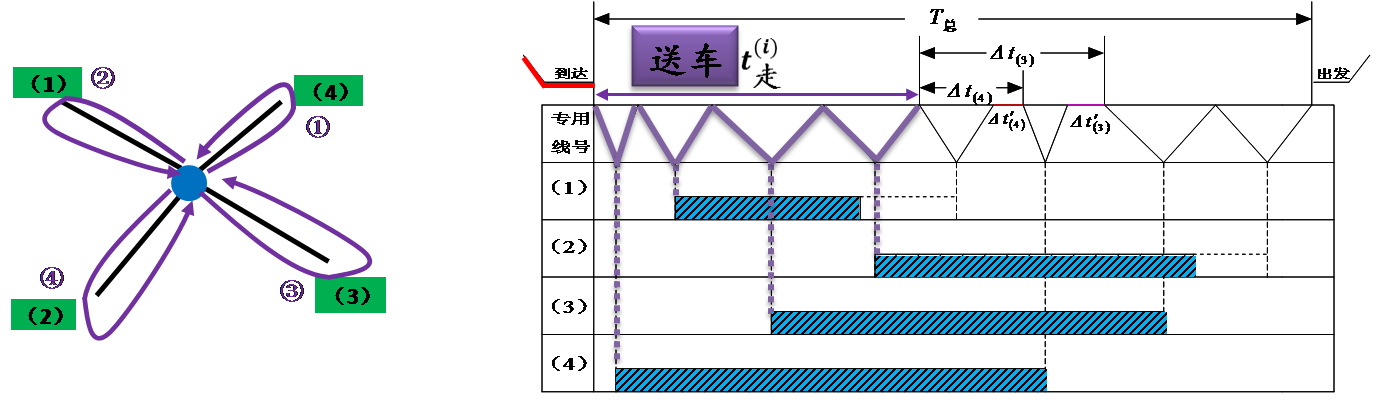
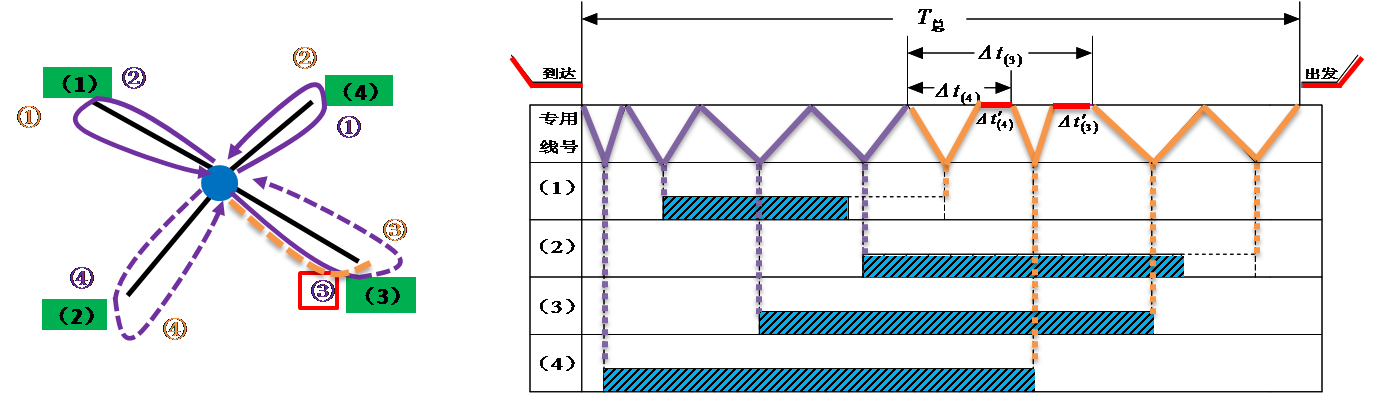
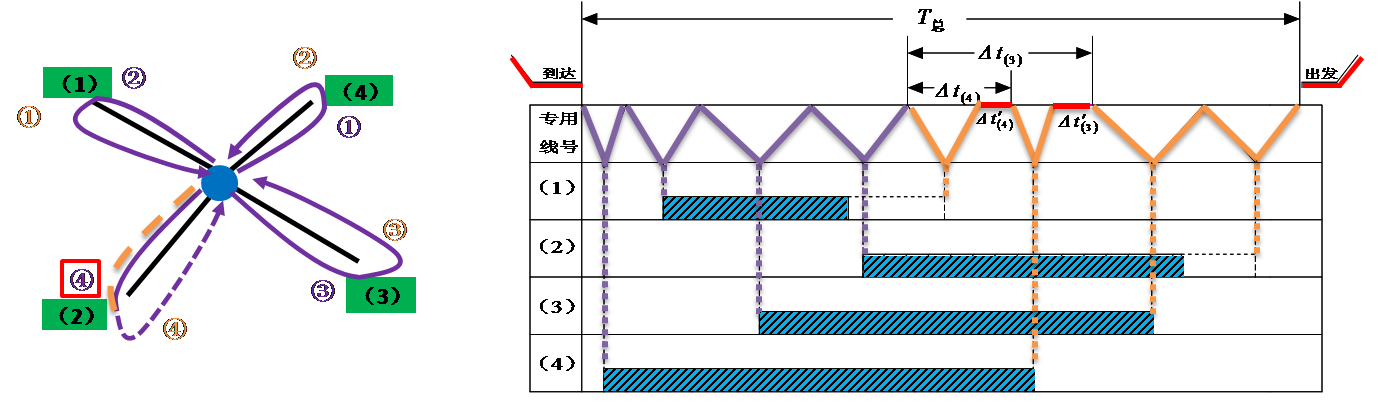
放射形专用线它的作业特点是：各线车辆的入线及取回站内的时刻是各不相同的，所以不同的送车顺序和取车顺序将会导致T总的不相等。

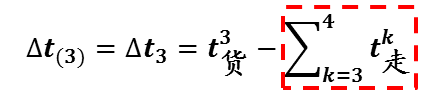
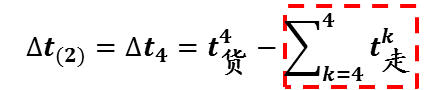
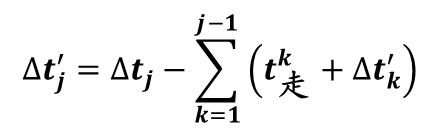
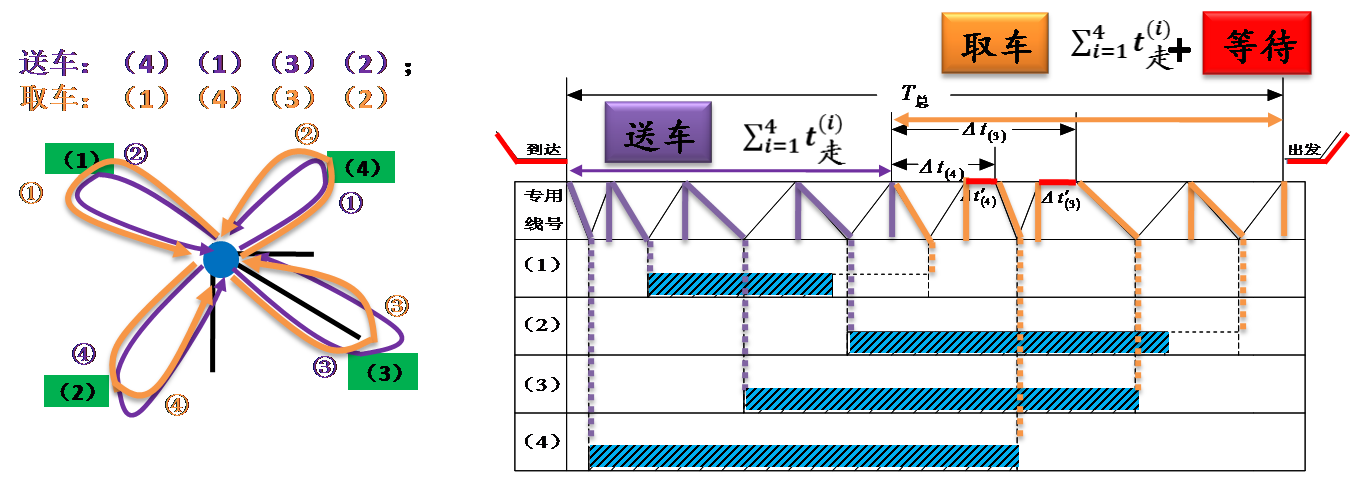
一个送车顺序和一个取车顺序配合而成的方案叫做一个取送方案。

一个取送方案用两个向量组成的集合来表示，第一个向量为送车顺序，第二个向量为取车顺序，向量中的数字为专用线代号。

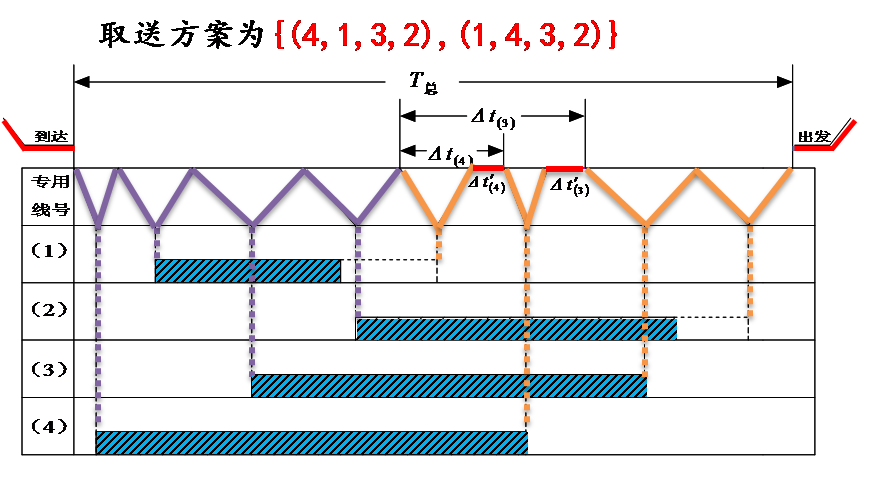
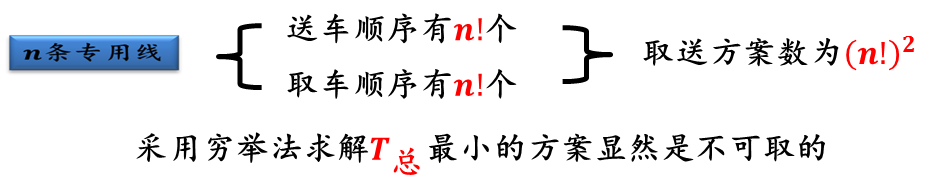
既然一个取送方案由送车和取车两部分组成，那么分部求解也许是一条有效的途径。

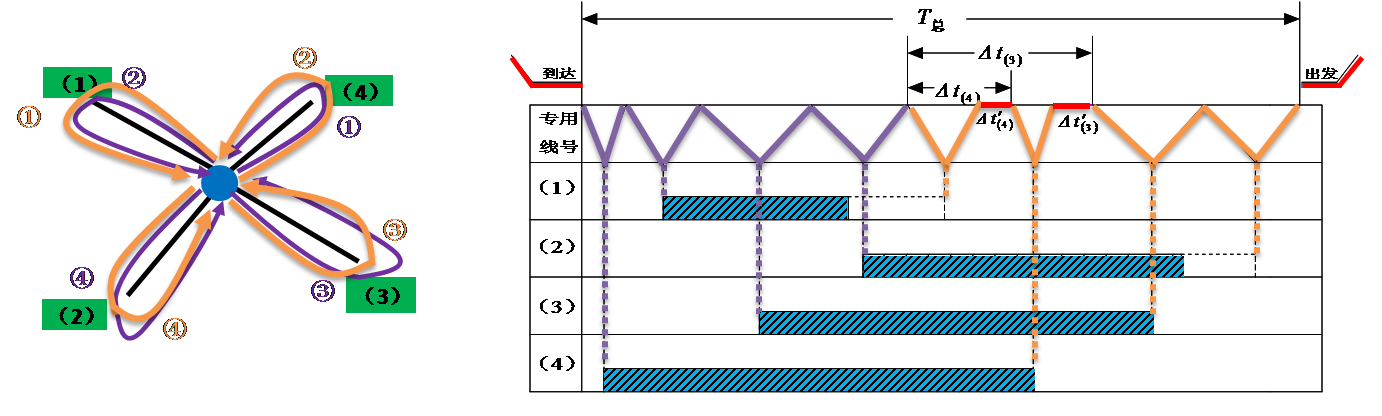
所谓分部求解，是指先不考虑送车顺序，而是假定送车顺序已经确定，在此前提下求解最佳的取车顺序。这一部分解决之后，再来考虑最佳送车顺序问题。

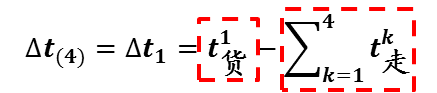
前人研究表明[1],在送车顺序已经确定的前提下，按照时差由大到小的顺序取车，将使得机车总的等待时间T总取得最小值。这便是确定最佳车顺序的方法—时间顺序法

这样，就把原来的问题规模由（n！）下降到n!。

余下的问题是如何方便地确定最佳送车顺序，对此至今尚未找到简单的算法。不过经验告诉我们，在需要送车的n条专用线中，先送t货最大的专用线是有利的。这样，需要比较的方案数可减少到（n-1）!。

求解最佳取送方案的步骤如下：

（1）列举(n−1)!个送车方案（即送车顺序）；

（2）对每一个送车方案

（3）在全部（n-1）！个方案中选择T等最小的方案，即为最佳取送方案。