第四节 圆形的透视（二）

所谓圆形物体主要包括圆柱，蝶状物，球体等，它们的透视和圆有这密切的联系，也与方体的透视有关系。

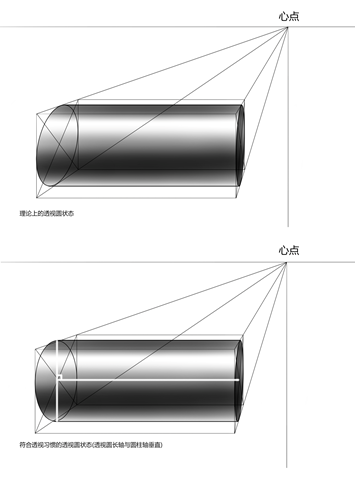
    1、圆物轴线与圆面长径的关系

圆柱和圆锥等都是有中轴的回转体，底面是圆形，在透视图中，地面成椭圆形状，中轴过底面直径中点，并垂直于底面长径。在透视图中，只有当中轴方向经过心点时，轴线与圆面长径保持垂直状态，这时的回转体看上去是端正的。如果轴线不经过心点，则轴线与圆面出现一定倾斜，看上去有点歪。从人们的观察习惯看，我们在看回转体时总是将中视线及心点对准轴线，所见物体端正舒适，并以此作为视觉认可的图像，对照片及透视图中边缘出现歪斜的回转体感到不舒服。因此，我们在画小型回转体或远处的回转体时，轴线与圆面的长径尽量保持垂直，视觉上会更和谐。画大型圆物或建筑物时，对应该发生的歪斜，要处理的有分寸。

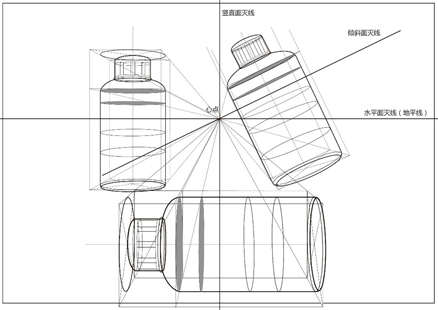
       2、圆面宽窄和柱面弧线的关系

 图中1，2圆柱体的圆面灭线分别是地平线和心点垂线，柱面所看到的弧线的弯曲程度以各自灭线为准。弧线离灭线远的弧度大，离灭线近的弧度小。3为任意放置的柱体，虽然不是标准位置，但是圆面灭线总是在柱体可见圆一侧，柱体可见圆面总是离灭线最近因此也就是弧度最小的。其他不可见圆面总是渐远渐宽，圆弧的弧度越来越大。圆柱4的圆面灭线横截圆柱，定和底的圆面都不可见，灭线上的圆弧成直线状，上下底的圆弧同样遵循离灭线越远弧度越大的原则。

 如图中所示的三个瓶子的瓶身和瓶盖都是圆柱体，三个瓶子的状态分别为竖直放置，水平放置和倾斜放置。竖直放置的瓶子的底面和瓶盖顶面的灭线是地平线，所有与瓶盖顶面和瓶子底面平行的截面的灭线都是地平线。竖直放置的瓶子被地平线分成上下两部分，地平线以上的部分我们可以看到截面的朝下方向面，地平线以下的部分可以看到瓶子截面的朝上方向的面。水平放置的瓶子的地面和瓶盖顶面的灭线是过心点的垂线，这条灭线将瓶子分成左右两部分，左边部分的瓶子截面可以看到朝右的面，右边瓶子的截面可以看到朝左的面。倾斜放置的瓶子的底面和瓶盖顶面的灭线是过心点的斜线，这条灭线同样将瓶子分成上下两部分，上半部分的瓶身截面能看到朝下的面，下半部的瓶身截面能看到朝上的面。

     

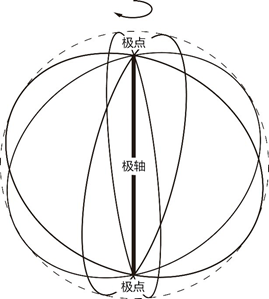
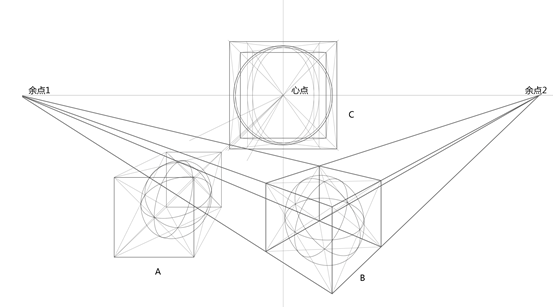
3、圆球的透视

圆球可以理解成是圆形沿任意直径进行旋转所得的封闭空间，这个旋转的直径我们称为极轴，极轴的两个端点称为极点，如图所示。在研究透视中的圆形时，我们是通过圆形外接正方形的透视来间接得到圆形透视的特点的，同理，研究圆球时可以通过圆球的外接正方体来间接得到圆球的透视特点。在前章研究正常视域部分时，我们提到在离开心点比较远的位置，即60度视锥以外的区域，正方体的透视形态发生比较剧烈的形变，并且这种形变会随着远离心点的距离的增大而愈加剧烈，正方体看起来被拉长，变成长方体，球体作为正方体的内接体，其透视也会随正方体一起发生相应的透视变化。如图8-8中的球体A的透视以外接方体平行透视的形式来研究，距离心点较远，处于有效视域的边缘，发生了明显的透视变形，圆球的外接正方体视觉上被拉伸成长方体，它的内切圆球也相应被拉长，视觉上成为“椭球体”。

课后作业：在同一场景中，绘制轮胎，拱门等虚体透视形态。