第三节 圆形的透视（一）

    圆面的透视在图形在产品设计草图中会经常用到，画好圆的透视图对于很多同学来说都是具有挑战性的，其实掌握了圆的基本特点后，透视方向的圆就不难画准了。

    和矩形方体相比，圆面的特征元素很少，我们很难从孤立的圆面对圆的透视进行准确的研究。所以，引入圆的外接正方形的概念，通过外接正方形的透视，间接研究圆面透视成为可行的方法。我们首先确定如何在正方形中画好内切的圆的平面图，我们知道，所谓内切于正方形的圆形，圆周上的四等分点与正方形四条边的中点是相切的。四个切点将圆周平均分成了四份，我们再确定每个圆周的中点位置就得到圆周上的八个关键点，然后用平滑的曲线连接这八个点就得到正方形内切圆的平面图了。1/4圆弧的中点我们可以通过将正方形边进行3：7分割，分割线与对角线的交点就是1/4圆弧的等分点。其中3：7的比例是经验值，我们记住这个比例就可以了。当然，几何功底好的同学可以试着证明一下。

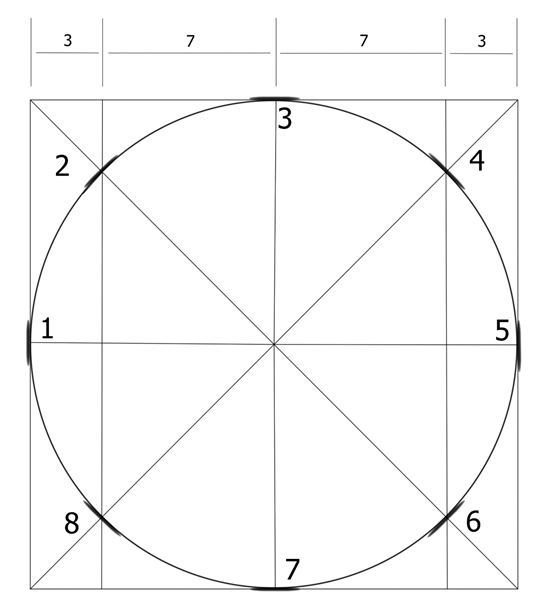
在平行透视方形内画透视圆

      由于圆周没有方向性，所以圆周在透视中没有平行透视和余角透视之分，平行透视和余角透视方框做出的透视圆效果相同。在平行透视方形中画圆同样确定余角透视方形的8个画圆关键点，然后徒手圆滑连接8个关键点即可。如下图所示。首先我们需要将方形的一条边进行3：7：7：3的分割，在余角透视情况下，我们只能通过量线的形式来进行分割。首先以近角点为端点做水平量线， 延长余点2至A点的连线使之与水平量线相交。我们设交点为A‘，我们将A’B进行3：7：7：3的分割，将分割点引线至余点2，那么这些线与方形对角线相交得点就是我们所需要的圆周上的4个点，另外四个点是各边的中点，我们可以通过从对角线交点引线至余点1和余点2的方法来获得，至此，8个圆周点都确定，随后可以进行徒手连接形成余角透视的透视圆。

              

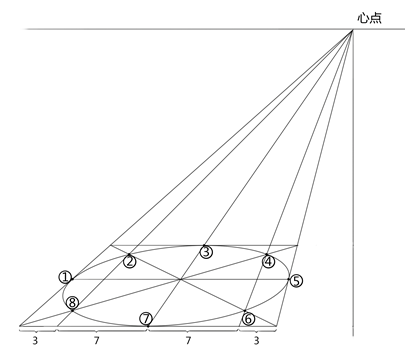
课后作业：

通过8点法画平行透视和余角透视中的正圆。