第三节 透视矩形的等分与复制

    

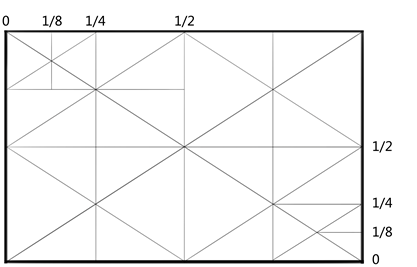
         在进行产品草图绘制的时候，我们常常需要做一些面积分割的处理（等分不等分的情况都有），比如音响功放的侧面按钮排布，卡车过个车轮的排布等，这些问题都可以归结为矩形透视的分割问题。我们首先来看一下如何画空间透视中矩形的中线，即如何两等分划分矩形的透视纵深。我们知道矩形的对角线相交于矩形的中点，利用这个原理可以很轻松地确定透视空间中的矩形中点，并随之对矩形进行纵深方向的等分分割。 如下图所示，利用矩形对角线等分特点可以快速得到矩形的1/2，1/4，1/8点。   

   

        

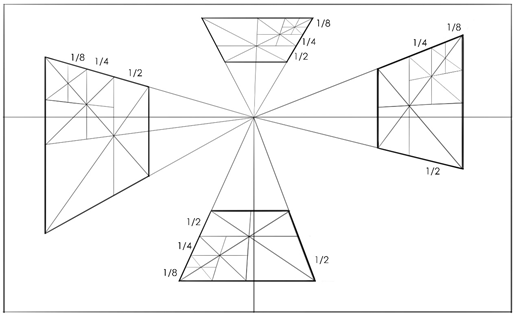
      在透视空间中，同样可以利用矩形的对角线等分特点将透视矩形进行分割，这种方法比距点法方便快捷，特别适合确定空间矩形等分点的位置，如下图所示。

       

课后作业：设计一组积木形态，并用矩形分割的方法把它表现出来。