第三节 余角透视深度测量

测点位置的确定是通过几何关系得出的。通过图Z48-2我们来分析一下测点法求余角透视长度的几何原理。图Z48-2是典型的方体余角透视状态下场景的顶视图，属于一般余角状态，方体两个竖立面与画面成角分别为α与β。自目点做两条射线分别与目线成角α和β，则两射线与视平线的交点E和D分别是方体两条余角边OB和OC的灭点。以OB边为例，过方体顶点O做水平标尺，此标尺与视平线及目线平行，作为测量工具。EF与EE1等长，连接FE1得到一个等腰三角形，顶角∠FEE1角度为α。射线FE1为自目点发出的射线，与视平线的交点是E1，可以看作是灭点寻求线，透视图中所有与FE1平行的直线的灭点都是E1，因此过B做FE1的平行线BA与水平标尺交于A，则BA就是透视图中自水平标尺向测点(E1)的引线，如果能证明OA与OB相等，就能说明测点法是合理的。由于AB与FE1平行，∠OAB与∠EE1F相等，∠AOB与∠FEE1相等都是α，因此，△OAB与△FEE1是相似三角形，那么△OAB也是等腰三角形，则OA与OB等长，由此可见，测点法在几何意义上是可以被证明的。

    

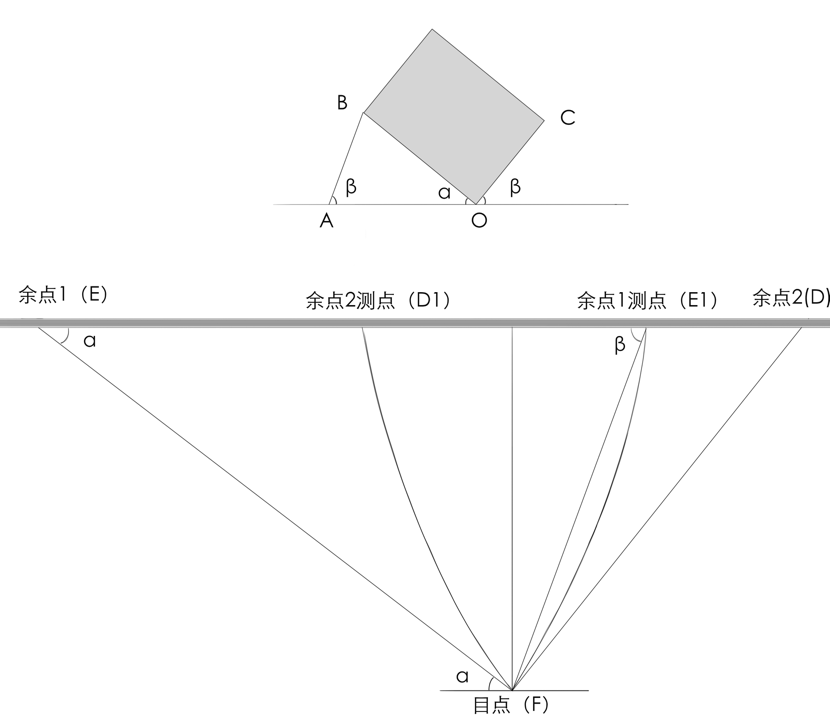
1.求测点：首先要找到两个余点对应的测点，以余点1为圆心，余点1到目点的距离为半径画圆弧，圆弧 与视平线的交点就是测点1，同样可以画出测点2.

2.  用测点：假如定视高为1，用测点做长和宽都为1的余角透视方形。自近角点o做水平量线OA和OB。由于我们定视高为1，因此，O点到心点的距离为1，将这个距离截取到OA和OB 上，自O点引线到余点1和余点2 ，所得线就是方形余点透视的方向。我们将OAhe OB的长度定位1，那么从A，B两点分别向测点1和测点2引辅助线，线与方形透视方向线的交点就是方形透视深度上单位1的位置线。从这两个位置再向余点1和余点2引线就完成了视高为1的透视环境中边长为1的方形的余角透视图。

课后作业： 设计一组方形积木形态，画出其余角透视图并用测点准确画出其透视深度。