第三节 透视缩尺法（一）

透视缩尺法基本原理   

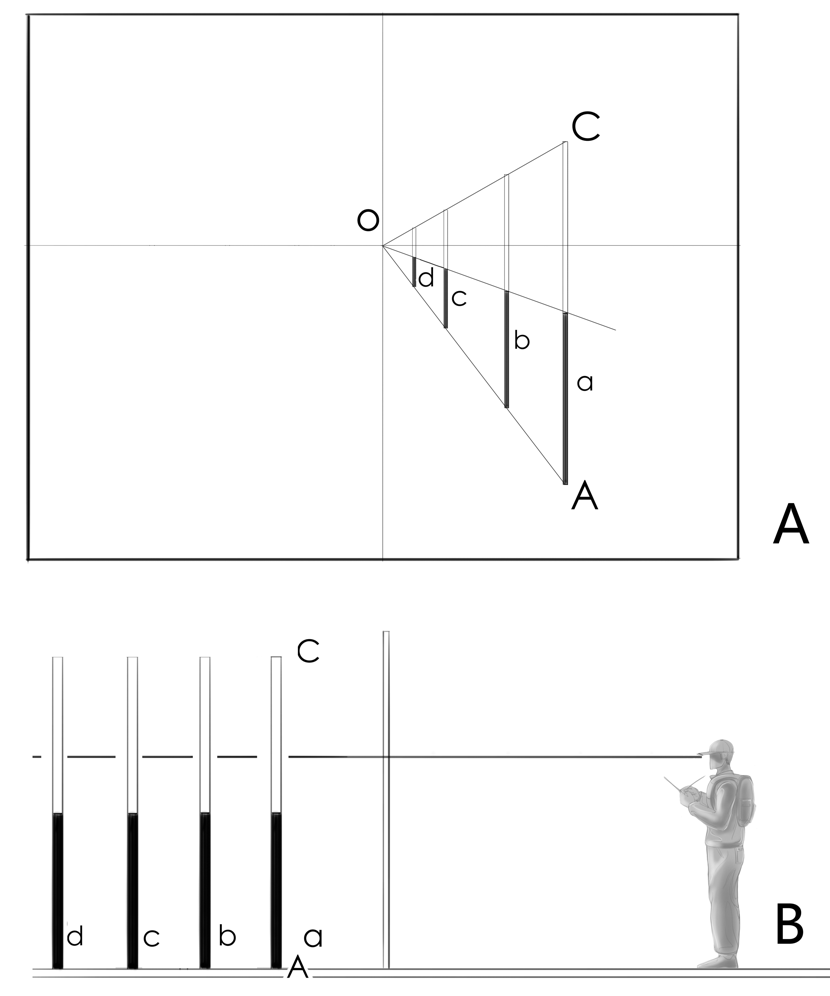
透视缩尺法是另一种寻求透视空间物体远近大小的方法，同视高法在本质上具有类似的理论基础。视高法是利用相互平行的平面间截得的平行线段等长的原理，而透视缩尺法则利用平行线间截得的平行线段等长的原理，可见“平行等分”是它们共同的理论基础，不同的是：一个是从平行面的角度思考，一个是从平行线的角度思考而已。如图所示，标杆a竖直立于画面中，自标杆的杆顶C和杆足A分别引 直线到心点o，则oA与oC为相互平行的一组直线。那么在直线oA上竖直放置等长的标杆b,c,d这些标杆的顶端都会卡在直线oC上，图Z114B是图A的侧视图，我们可以看到oA与oC是平行关系，因此它们之间截得的竖直线段是相等的。在画成排的路灯的时候，透视缩尺法是很好的方法。

    

课后作业：用透视缩尺法画停车场上不同远近的车辆。