第二节 俯视和仰视透视方向与灭点寻求

俯视和仰视方体透视方向

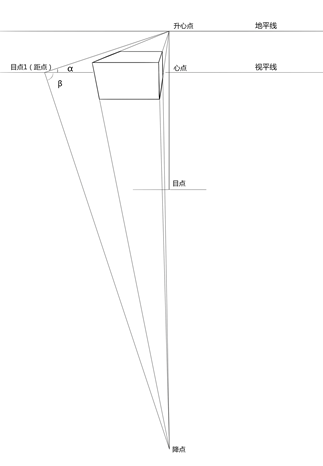
平行俯视图由于视向从原来的平视变为向下倾斜，画面跟随视平面倾斜相同的角度，不再与地面垂直。使得原本与画面垂直的平变线不再与画面垂直，因此，它的灭点也就不再是心点了，但它和地平面的关系没有变，仍然平行于地平面，因此它的灭点仍然在地平线上，叫升心点。方体上原本平行于画面的竖直原线现在成为变线，在画面中汇聚向降点。原来的水平原线还保持水平，不发生汇聚，没有灭点。

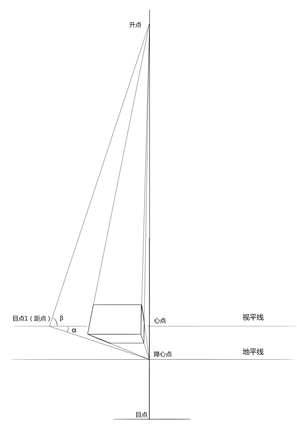
平行仰视与平行俯视很相似，不同的是画者视向向上倾斜，因此方体原本的竖直原线开始向上发生汇聚，指向升点，原本垂直画面的变线汇聚向降心点，降心点也同样在地平线上，是地平线和过心点垂线的交点。

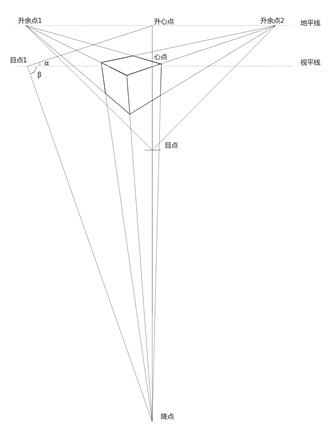
余角俯视画面，是在余角透视的基础上将视向往下偏转一定角度，造成物体原来的垂直原线成为变线，灭点在过心点的垂线上，由于视平线向下移动，与地平线分离，原本汇聚向地平线上余点的两组平变线不受视向变化的影响，仍然指向地平线上的余点，由于此时视平线压低，与地平线分离，透视图中，地平线在上，视平线在下。所以地平线上的余点称为升余点。原来平视时垂直于地面的垂直原线现在成为变线，汇聚向过心点垂线上的降点。

       

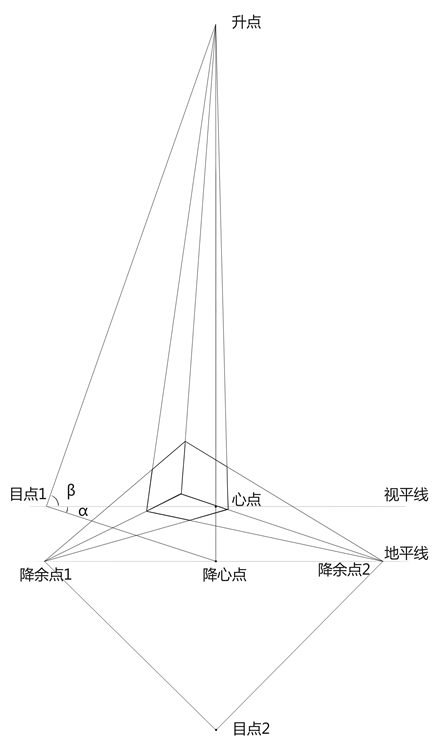
余角透视仰视的情况与余角透视俯视的情况很相似，只是视向由向下改为向上，在透视图中造成视平线在上，地平线在下。于是平视时的两个余点称作降余点，平视时的垂直地面原线变成向上汇聚的变线，灭点为过心点垂线上的升点，在过心点的垂线上。余角俯视和余角仰视的方体都具有三个灭点的，因此又称三点透视。

                                                                                                                                                                                                                                                               课后作业：以玩具火车为模型，绘制俯视和仰视的灭点寻求图例，要求作图过程完整。