第二节 视高法（二）

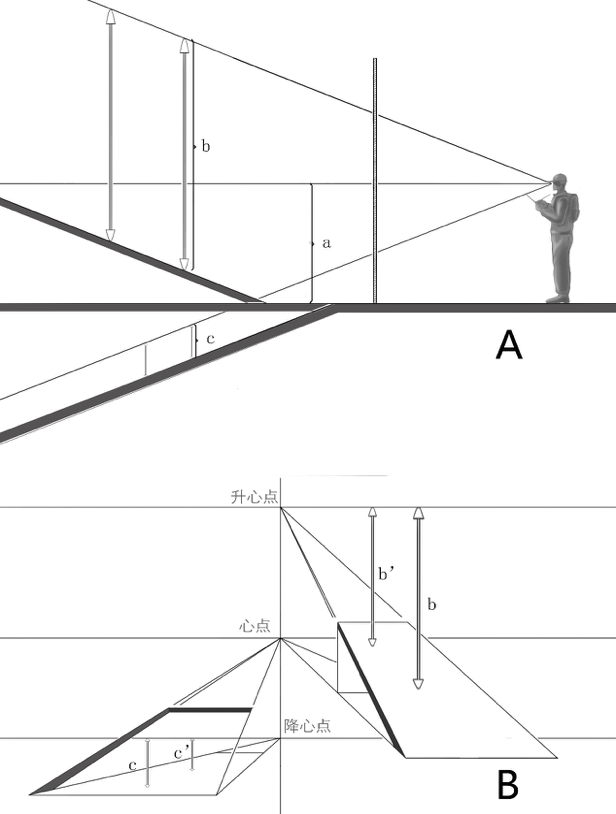
确定斜面上的物体高度，同样可以采用视高法，如果水平面上的视高法可以理解成水平面和它的灭线间分割的平行线段相等，那么套用水平面视高法的原理来分析，斜面视高就是透视图中，斜面上任意一点到斜面灭线的竖直距离相等。斜面上的视高法以斜面的灭线为标尺，斜面其实并没有什么神奇之处，我们可以想象眼前的地面形成了坡面，可以是上斜坡或者下斜坡，那么原来的地平线作为灭线就不适用于斜面了，因此要改为用斜面的灭线来代替。除了基面由平变斜，灭线由地平线变斜面灭线外，其他原理仍然遵从视高法原则。图Z113中的A是斜面视高研究的侧视图，a线段的高度就是水平地面的视高，即一人高。b线段的长度为上斜面视高，c线段的长度为下斜面视高。通过测量我们得出，b线段长度是a线段长度的2倍，因此上斜面的视高是2倍人高，c线段长度是a线段的1/3，因此下斜面的视高就是1/3人高。图Z113的B图是画者所看到的透视图，各个基面上的视高就是基面上任意一点到基面灭线的竖直距离。在确定了上斜面和下斜面的灭线位置后，我们得出，cc’两条线段的透视高度是1/3倍人高，bb’两条线段的透视高度是2倍人高。

     

              

课后作业：尝试画斜面上的几个不同大小的产品，如坡路上的车辆与行人。