第二节 关键概念分析

1.视距

视距是视点到画面的距离，每一张图画都有自己固定的视距，在画同一张图的过程中，视距始终保持固定不变，只有这样才能顺利运用所有透视原理进行绘图。视距的大小直接决定了透视图的画面内容和透视剧烈程度。通常我们可以通过固定画者和被画物体，改变画面的位置来改变视距。也可以通过固定被画物体与画面，改变画者位置来改变视距。这两种视距变化的情况会产生不同的画面透视效果，我们来通过具体图例进行分析。

第一种情况，画者和被画物体位置不变，只改变画面的位置来改变视距，相当于画者和被画物体间放置的玻璃前后位置发生了变化，而他透过玻璃看到的物体不会发生变化，他甚至都察觉不到透明玻璃发生了位置变化（我们假设透明玻璃无限大且完全透明）。因此这种情况的视距改变对透视没有任何影响，两幅不同视距的图画的唯一区别是画面范围的变化，取景框大小不变的情况下，取景框越远离画者，取景框中所囊括的物体范围越小，反之越大。

第二种情况是画面和物体保持位置不变，改变画者的前后位置，从而改变视距。这种情况相当于改变了画者和被画物体的距离，大家记住，这个距离的改变在人眼凸透镜成像原理的基础上，一定会改变物体在人眼中的成像形式，因为凸透镜的物距改变了，于是形成透视的变化。由于画面和被画物体之间固定不变，因此，画面内的内容不变，但随着画者离开画面的距离增大，画面会呈现长焦镜头的效果，画面的纵深感变短，画面的透视程度变得缓和。相反，当画者向画面靠近时，画面呈现广角镜头的特性，即纵深感变强，画面的透视程度变的剧烈。视距越远，画面的透视状态越接近平面化。如图9所示,A图为远视距下的产品透视图，视觉感受平稳舒适。B图为缩小视距后的透视效果，此时，画者的离汽车非常近，大概在1米的范围左右。此时的近视距造成物体发生剧烈的透视，车身的部分边线开始发生倾斜。

                           

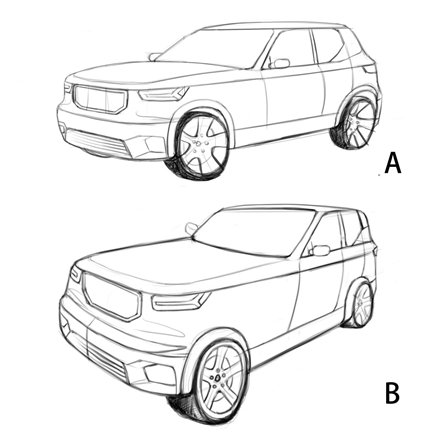
图9

2.正常视域

    

什么是视域，顾名思义就是视力所及的区域，我们人类的眼睛虽然长在头的正前方，却可以看到头前方水平方向188度左右扇形面积内的物体，竖直方向140度左右扇形区域内的物体，这个区域几乎囊括了人正面的所有空间。这种有趣的生理结构可能是来自于祖先的进化，毕竟看的范围大一些能够更早地发现猎物或者危险。很多动物的视域甚至更夸张，比如马，它的眼睛长在头的两侧，视域几乎涵盖360度，真正做到全方位观察敌情。所以不要以为站在马后它就发现不了你，很危险的哦。人的视域分布图如图11所示。

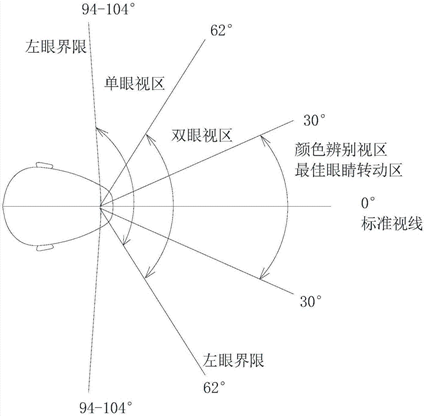
                                                     图 11

 

 人的视域虽然比较宽，但是这个巨大的空间范围并不是所有的物体我们都能够真正看清楚的。大家都有这样的经验，你在剧场座椅上看舞台表演，你对舞台上演员观察的很清晰，这是你旁边的空座位来了一个新的观众，你在没有把头转向他时，你已经用余光看到有人坐在你的旁边了，但是这个人是谁，是男是女，你认不认识，这些信息需要你把头转向他（她）你才能确认，而你头转向他后，确认了来的是你的同学小满，你的余光仍能看到舞台上的表演，却不能确定演员的具体动作和角色位置了，因为此时，你是用余光在看舞台。由此可见，我们的视域虽然很宽阔，但是真正可以捕捉有价值信息的视域是有限的，这个有限的区域我们叫做“正常视域”，也是我们在进行绘画和绘图时需要图面保留的区域。“正常视域“内的景物光线投射到我们的视网膜上时会留下清晰而明确的景物形态像。我们假定人眼是单眼，那么这个”正常视域“就是以人眼为顶点的顶角为60度的圆锥，在这个圆锥内的物体，在一定距离之内，理论上人是可以清晰准确地看到的，并能够确定其完整而明确的像。这个顶角为60度的圆锥我们称之为”视锥“。视锥和画面相交部分为圆形，我们一般以这个圆的内接矩形作为我们的取景框。

由于人的视网膜是弧形球面，于是靠近正常视域视锥边缘的部分，成像的形变就会越剧烈，即直线会有变弧线的趋势。而我们在进行透视图的作图法时，直线始终是按直线处理，不做迎合视网膜成像的调整，因此，我们绘制的透视图理论上我们看到的物体形象会有些许的差别，特别是在正常视域以外的部分，由于这部分图像一般不在我们的取景框内，因此，这些许的差别可以忽略不计。但我们可以利用我们肉眼的成像特点，在需要特殊效果（如夸张的鱼眼镜头效果）时，可以适当强化这种变形，使画面更生动。这种效果图在产品宣传，设计竞赛板式设计等场合可以很好地加深观者的印象。如下图所示。

  

 

                              

 

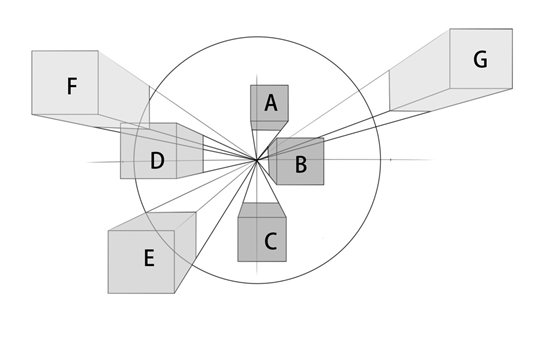
在取景框位置和大小不变的前提下，视锥顶角的大小实际上就是视距变化的结果，从下图我们可以了解到，随着视距的增大，视锥顶角逐渐变小，我们以心点至取景框最远一角的距离为半径画圆，我们可以认为此圆就是对应此取景框的视锥与画面的交线。我们假定这个圆的半径为R，那么视锥的高就是视距。根据几何作图法我们知道，当视距为R时，视锥顶角为90度，显然已经超出正常视域的范围，说明我们此时看到的取景框里的图像会产生很大的变形。画者远离画面，继续增大视距，当视距分别是2R，3R，4R时，对应的视锥的顶角分别为53度，37度和28度。我们发现随着视距的增大，取景框开始进入正常视域内。随着视距的增大，取景框中物体的透视会变得越来越平缓，物体被拉伸和变形的情况会越来越小。

                        

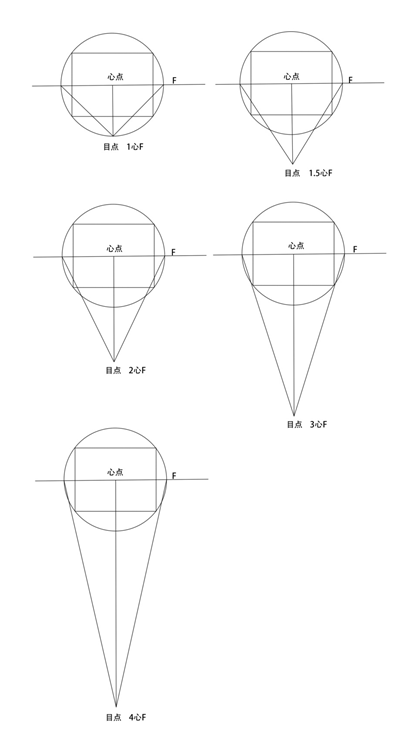
下面我们通过一张产品草图开观察不同视距下的透视图面变化。从图中我们不难看出，在视距很近时（一倍R），物体发生了很的拉伸和变形，特别是取景框四周的物体，视觉上改变了原有的比例，而随着视距的增大，产品的透视拉伸越来越小，整体的纵深感也越来越小。我们可以设想一下，如果我们的视距变成无限远（假设我们的视力足够好，人可以看清画面），那么我们看到的取景框中的物体的平行线将无限接近于平行，不发生任何汇聚，平行透视的纵深感接近零，即我们所说的正视图。有兴趣的朋友可以再把视距拉远画几张图就能体会我所说的了。

               

 

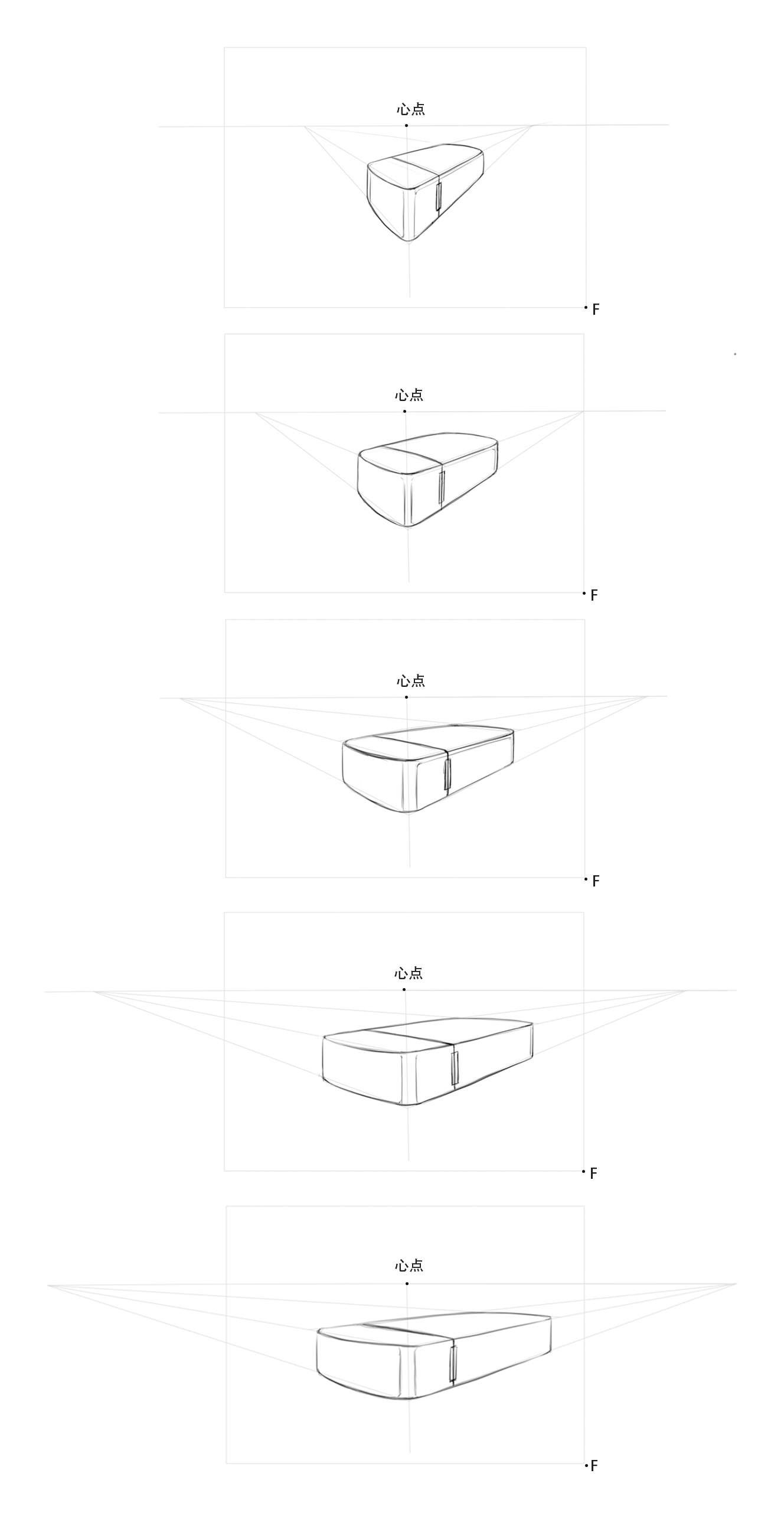
通过图例我们可以得出的结论是，在同一个取景框的前提下，视距近则物体的纵深感强，透视剧烈，物体变形的趋势明显；视距远，则物体的纵深感若，物体透视缓和，有被压缩的感觉。大家可以尝试把一个物体放在眼前很近的地方感受下，比如你心爱的的手机，当它放到快贴近你鼻子的时候，是不是看上去有很长的纵深感，像个万吨巨轮在超你驶来。

 

3.地平线和视平线

地平线和视平线都是存在于画面上的线，是我们在进行透视图的绘制过程中必不可少的参考线。我们的生活经验中地平线是眺望远方时，天地相接的那条线。在平静的海边，天海相接的地方会有一条水平的分界线；在一望无际的草原，沙漠，远方同样会有一条天地交界线；即使是在城市，如果你站的足够高，眺望远方时同样能看到蓝天和地面在远方相汇合的那条边际。在透视系统中，地平线是过画者眼睛的水平面与画面的交线。视平线是我们为了研究透视原理而创造的一条线，在现实生活中很难察觉到它的存在。我们前面提到过视

      平面与画面永远是垂直相交的（还记得那个电焊小哥么？）那么，它们的交线我们就定义为视平线。在画者平视的时候视平线和地平线是重合的。当画者仰视时，视平线在画面的上方，地平线在画面下方。当画者俯视时，地平线在画面上方，视平线在画面下方。当画者垂直仰视或垂直俯视时，画面中只有视平线，没有地平线。所以我们可以这样理解：地平线的个性是顽固的，它是过画者眼睛的水平面和画面的交线，它的水平面属性永远不会改变，无论画者的视向如何，它都不会屈从与画面。当画面与水平面平行的时候（垂直俯视和垂直仰视的情况），它干脆在画面中消失。而视平线则更加依附于画面，由于它是画面和视平面（而非水平面）的交线，因此，无论视向如何，视平线总是在画面中，它需要被画者关注，它需要观众的凝视。图16是几种不同视向时画面中地平线和视平线的位置说明。

                               

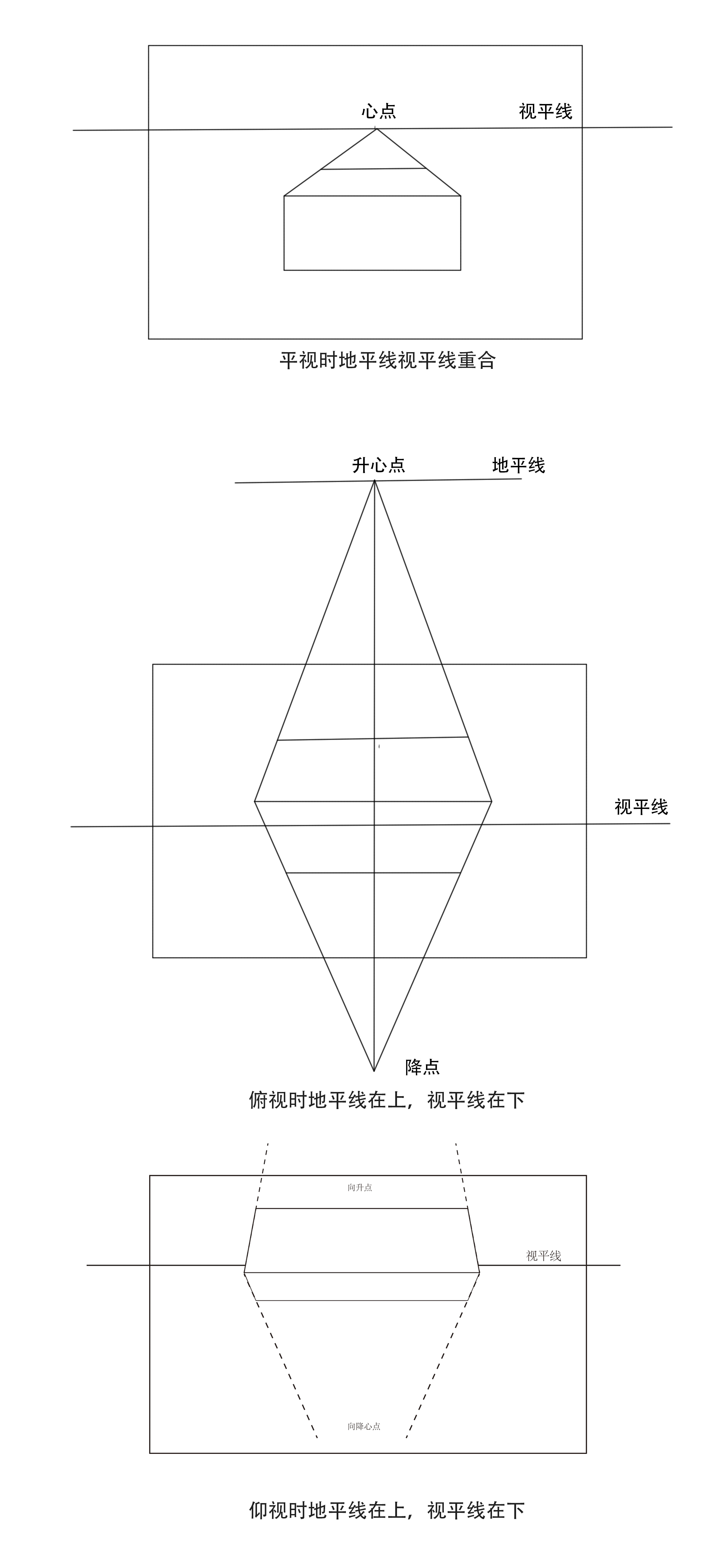
        地平线在画面中起到了参考线和标尺的作用，在透视的画面表现中，地平线控制着物体水平面和水平线段的透视状态。地平线是所有水平面的灭线，所有与水平面平行线的灭点都在地平线上。画面中地平线以下的水平面我们可以看到它的顶面，地平线以上的水平面我们可以看到它的底面，刚好处在地平线位置的平面既看不到顶面也看不到底面，程一条水平线。等大的水平面，在画面的垂直方向上越接近地平线，所展现的面积越小，越远离地平线，所展现的面积越大。这一规律在我们进行产品草图表现的时候非常有用，地平线的位置可以很好地为我们划分水平物体的位置，地平线分割水平面位置的原理其实和其他灭线与相应平面的原理相一致，这点我们在后面论述灭线的时候会着重介绍。

视平线是所有与视平面平行的平面的灭线，这些线我们叫做平线，即与视平面平行的线。除此之外所有与视平面不平行的线我们叫做斜线，他们的灭点在视平线上或者下，分别叫做升点和降点，其中与视平面垂直的线我们叫做竖线，因为垂直于视平面所以必然平行于画面，所以属于原线，没有灭点。视平线也是所有平行于视平面的平面的灭线，作为灭线，视平线同样担当着分割平面位置的作用，所有平行于视平面的平面中，在视平线以下的我们都能看到顶面，在视平面以上的我们都能看到底面，刚好处在视平线位置的平面我们只能看到一条线。多数情况下我们画图的视向是水平的，造成视平面是水平面，地平线与视平线重合。当视向发生改变，画者改为仰视或俯视时，地平线与视平线分离，此时视平线与地平线仍然各自担当着灭线的职责，图面中的平面即线段也都各自遵守着与它们的位置关系。

4.原线变线和灭点

    

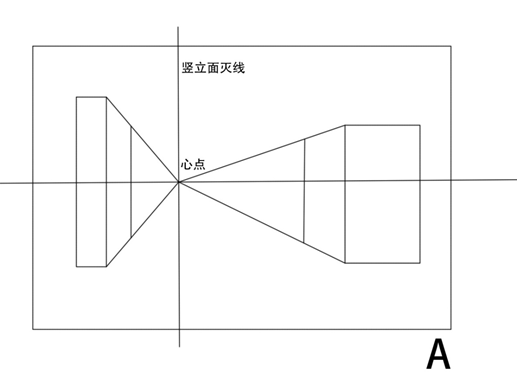
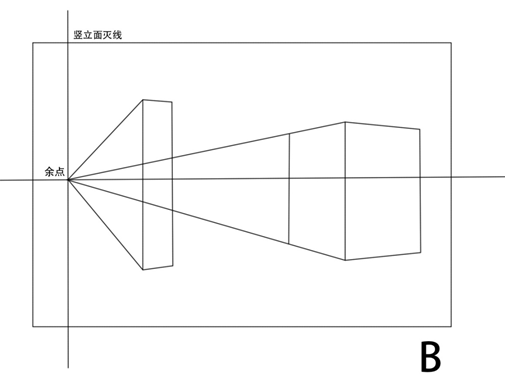
       透视学的研究重点之一是平行线发生汇聚的规律，我们首先将画面中的线进行划分，哪些平行线会发生汇聚，哪些不发生汇聚。通过几何原理，我们发现，所有与画面平行的线，在画面中任然保持自己的方向并且一组平行线同样保持平行，不发生汇聚。所有与画面不平行的线我们称之为变线，变现在画面中的透视方向与空间中的原方向不同，相互平行的变线在画面中汇聚向同一个灭点，其中垂直于画面的变线的灭点是心点。与画面不垂直但与视平面平行的变线的灭点在视平线上，我们称之为余点。其余的既不与视平面平行，也不与画面垂直的变现的灭点分别是升点和降点，其中向视平线上方倾斜的成组平行变线汇聚向升点，向视平线下方倾斜的成组平行变线汇聚向降点。我们通过下图来系统了解原线和变线。

                                  

 

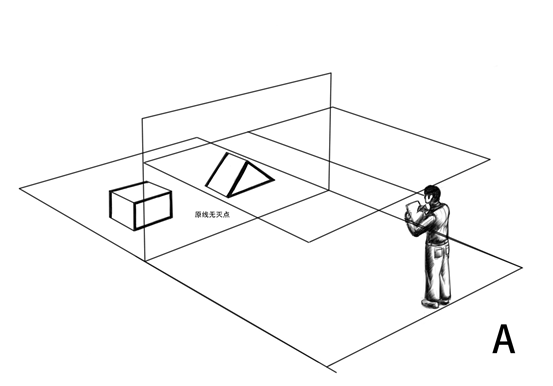
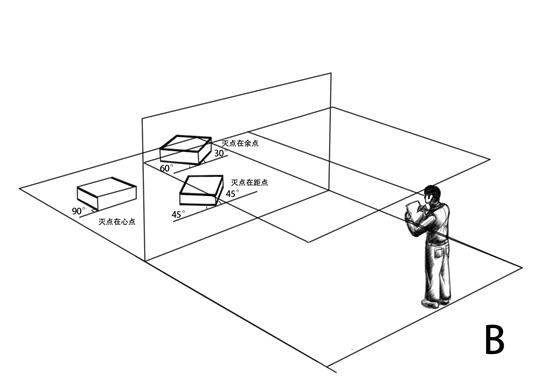
下图总结了具有代表性的变现的灭点位置特征

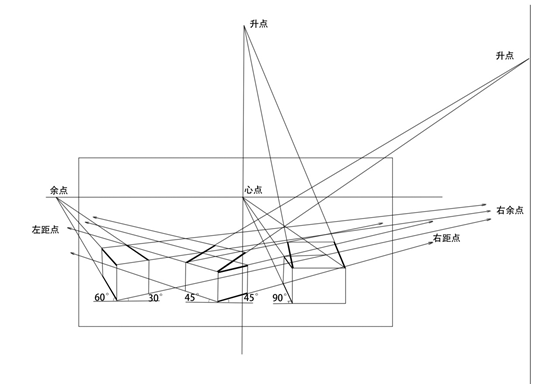
                                                                               图19

5.灭线  

    

       灭线是和灭点相关联的概念，与画面不平行的平面，在无限远处都会消失在一条线上（就如地平面在远处消失在地平线上一样），这条消失线我们称为这个平面的灭线。我们也可以把灭线理解成灭点的集合，即这个平面上的所有直线的灭点的集合，形成了这个平面的灭线。我们前面提到过的地平线，视平线都是灭线。一组平行的平面它们拥有公共的灭线，且此灭线对这组平面的位置分割起到关键作用。在灭线两侧的平面分别可以看到平面两个不同的面，在灭线上的面呈直线状，看不到面。拥有共同灭线的等大平行平面，离灭线近的看上去窄，离灭线远的看上去宽。

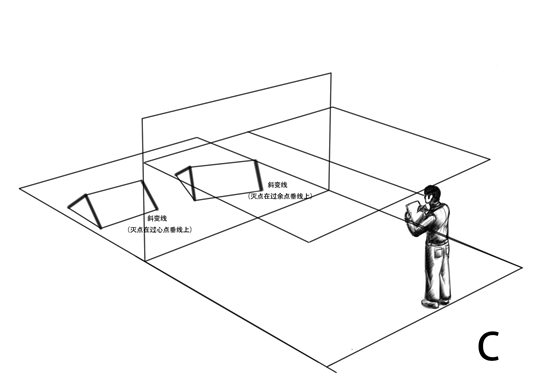
      灭线位置的寻求：要寻找一个物面的灭线，理论上可以过画者眼睛做一个平行于该物面的平面，这个平面与画面的交线就是该物面的灭线。以下是几种寻求灭线的图例。

                            

                             

课后作业：搜集产品表现照片或图样，分析画面中所涉及的今天所讲的透视元素。