第一节 视高法（一）

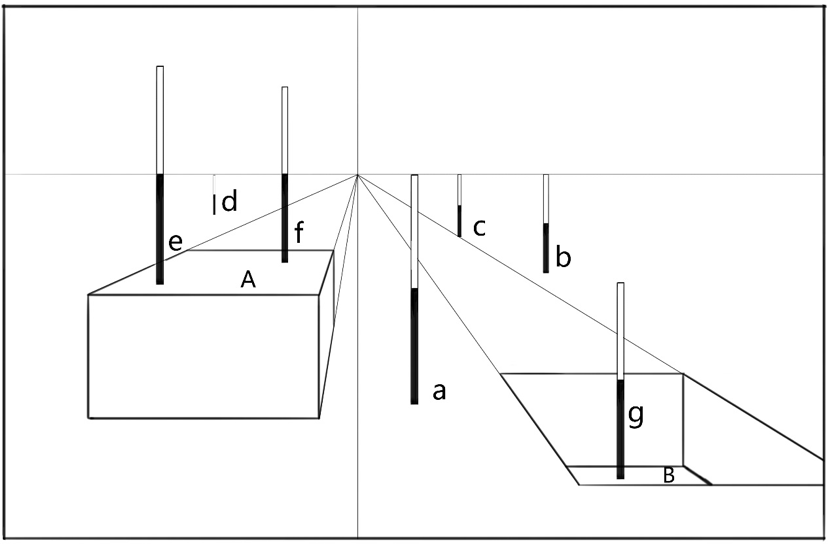
        透视视高法，顾明思议是通过透视视高来确定透视画面中不同位置物体的高度的方法。我们在前面的透视系统中认识了视高，它是指在透视画面中，被画物体所在的基面（地面，台面或桌面等放置物体的平面）与基面的灭线之间的竖直高度，如果是平视地面上的物体，视高就是地面到达地平线的竖直距离。如图Z110所示的透视场景中，几根尺寸相同位置不同的直立黑白杆分别置于地面，台面以及坑底，画者平视。那么地面，平台和坑底就是不同的基面，每个基面对应不同的视高。其中平台顶面A到视平线的竖直距离是1/2黑白杆高度，即基面A的视高是1/2杆高。所以，放置在平台A面上的竖直棍杆的1/2处位于视平线上。

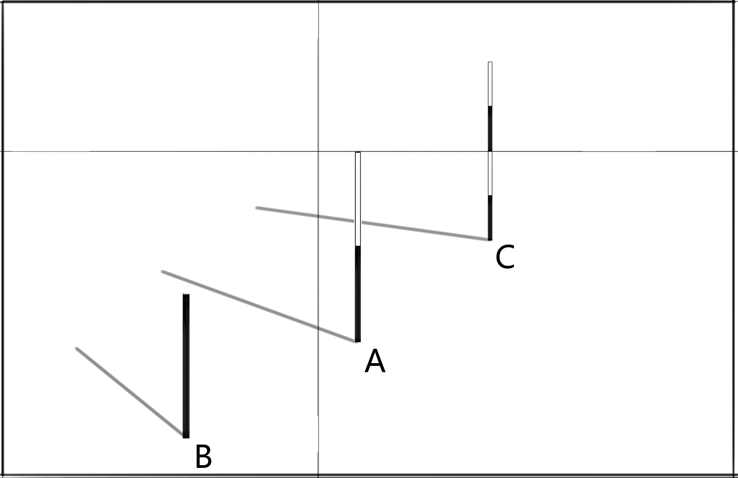
        视高法以视平线为准绳，以视高为标准量进行竖直空间高度的等比例测量。在视高确定的情况，我们就可以根据物体实际大小和视高的比例关系来确定透视空间中物体的竖直高度。如图Z111所示，视高为1人高，三根竖直放置在地面上的棍杆距离画面远近不同，高度不同。三棍杆都是垂直于地面的原线，不发生透视汇聚与缩减，竖直方向的比例是可测的。B离画面最近，A居中，C最远。A棍高1人高，顶端刚好与地平线齐平。B棍为1/2人高，棍杆顶端达不到视平线位置，在棍杆立足点到视平线1/2高的位置。棍杆C为2倍人高，在透视空间中，视平线刚好卡在它高度的1/2处，视平线上下两端棍杆相等。由此可见，在视高法中，视高作为1倍量，以地面到视平线的竖直线段高度来标注，物体的透视高度根据与视高的比例相应进行计算即可。物体高度小于1倍视高，则物体最高点在视平线以下，大于1倍视高则最高点在视平线以上，刚好为1倍视高，则高点与视平线平齐，这个原理和之前我们学过的地平面线作为地面灭线，对水平面的朝向分割原理是统一的，大家可以结合在一起来理解。

 课后作业：通过视高法画出桌面上放置的5个以上大小不同的文具。