定点数的补码加法
运算方法
任意两个数的补码和等于这两个数的和的补码。
[X]补+[Y]补=[X+Y]补
说明
符号位与数值位按同样规则一起参与运算， 符号位运算产生的进位要丢掉，结果的符号位由运算得出。
举例
例 1: X＝-0.1011 Y＝-0.0100，求 X+Y＝？
解: [X]补=1.0101，[Y]补=1.1100
[X]补+[Y]补=1.0101+1.1100=1 1.0001（符号位产生的进位通过模2加的方式丢掉）
[X+Y]补=1.0001
X+Y=-0.1111
定点数的补码减法
运算方法
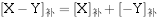
即：任意两个数相减的补码等于被减数的补码加上减数相反数的补码
说明
(1)(-Y)的补码称为[Y]补的机器负数。由[Y]补求[-Y]补的方法是，不管Y的真值为正或为负，都是将[Y]补的各位连同符号位在内全变反后，最低位加1。
(2)符号位与数值位按同样规则一起参与运算， 符号位运算产生的进位要丢掉，结果的符号位由运算得出。
举例
例 1: X＝-0.1011 Y＝-0.0100，求 X-Y＝？
解: [X]补=1.0101，[Y]补=1.1100， [-Y]补=0.0100
[X-Y]补=[X]补+[-Y]补=1.0101+0.0100=1.1001
X-Y=-0.0111
溢出及其判别方法
在计算机中，由于机器码的尾数通常是给定的（如16位字长，32位字长），因此，在计算机中数的表示范围是有限的，若两数进行加减运算的结果超出了给定的取值范围，就称为溢出。一旦出现溢出，必须及时处理，否则会出现错误。
假设:
被操作数为：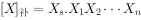
操作数为：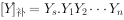
其和（差）为：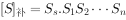
采用单符号位的判断方
两异号数相加或两同号数相减决不会产生溢出，仅当两同号数相加或两异号数相减时才有可能产生溢出。
两同号数相加时，如果结果的符号与参与运算的操作数符号相反，则表明有溢出；两异号数相减时，如果结果的符号与被减数的符号相反，则表明有溢出。
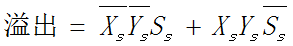
采用双符号位的判断方法
一个符号位只能表示正、负两种情况。当产生溢出时，符号位的含义就会发生混乱。如果将符号位扩充为两位（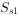
和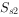
），其所能表示的信息量将随之扩大。既能检测出是否溢出，又能指出结果的符号。
每个操作数的补码符号用两个二进制数表示，称为变形补码，用“00”表示正数，“11”表示负数，左边第一位叫第一符号位，右边第一位称为第二符号位，两个符号位同时参加运算，如果运算结果两符号位相同，则没有溢出发生。如果运算结果两符号位不同，则表明产生了溢出。“10”表示负溢出，说明运算结果为负数，“01”表示正溢出，说明运算结果为正数。
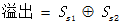
利用进位值的判断方法
两数运算时，产生的进位为：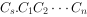
其中，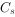
为符号位产生的进位，
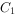为最高数值位产生的进位
两补码数进行加减运算时，若最高数值位产生向符号的进位而符号位不产生进位时，发生正溢出，若最高数值位无进位而符号位有进位时，发生负溢出 。
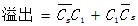
所谓正溢出，即超出机器所能表示的最大正数。
所谓负溢出，即超出机器所能表示的最小负数。
加减法溢出的条件总结
| 操作 | 操作数A | 操作数B | 表示结果有溢出的条件 |
| A+B | ≥0 | ≥0 | <0 |
| A+B | <0 | <0 | ≥0 |
| A-B | ≥0 | <0 | <0 |
| A-B | <0 | ≥0 | ≥0 |
