一、基本假设

（1）两部门经济社会社会（2）储蓄函数为，s为储蓄率。（3）劳动力按照一个不变的比率n增长。（4）折旧率为    （5）假设社会人口都是劳动力人口（6）生产的规模报酬不变（7）暂时不考虑技术进步。

二、基本方程

根据以上假定，设生产函数为

由假定（6），有。λ为正数。令，有。式中，N为全部人口，为人均产量（以y表示），为人均资本（以k表示）。于是，表达式可写为

 

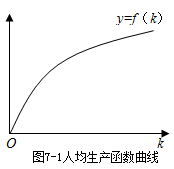从式中可以读出：取决于。

即：人均产量取决于人均资本量，人均资本量的增加会使人均产量增加。但是，由于边际报酬递减规律，随着人均资本量的增加，人均产量会以递减的速度增长。但是，人均资本量的增加——或者说人均资本增长率又取决于什么？

在一个只包括家庭部门和企业部门的简单经济中，经济均衡的条件为：

即投资或资本存量的增加等于储蓄。资本存量的变化等于投资减去折旧。当资本存量为K时，假定折旧是资本存量K的一个固定比率δK（0＜δ＜1），则资本存量的变化△K为

                                （7.6）

根据 ，（7.6）式可以写为：

                               （7.7）

（7.7）式两边同除以劳动数量 ，有

                                           

另一方面，注意到（7.8）式有存在，对两边取对数，则有，又因为这些变量都是时间t的变量，即，对该式两边求关于时间t的一阶导数，得

                             （7.9）

（7.9）式中的，n为劳动增长率。于是该式用文字来解释就是，人均资本增长率＝资本增长率－劳动增长率。

（7.9）式两边同乘以K并移项，有：，推出

                           （7.10）

（7.10）式两端同除以N，则有：           （7.11）

将（7.8）、（7.11）式合并，消去，于是

，

                            （7.12）

式就是索洛经济增长模型的基本方程，式中，sy为人均储蓄，△k为人均资本增量。（n+δ）k由两部分组成，一部分是nk，即人均储蓄中用于装备新增劳动力的花费，另一部分是δk，即人均储蓄中用于替换旧资本的花费，即人均折旧量，（n+δ）k被称为资本的广化。人均储蓄中超过资本的广化的部分会使得人均资本增多，即△k＞0，△k就是资本的深化。因此，索洛增长模型的基本方程可以表述为：人均储蓄是资本深化与资本广化之和，或者说，人均储蓄用于资本深化与资本广化两部分。

（7.12）式用文字解释就是，人均资本增长＝人均储蓄－（人均储蓄中用于装备新增劳动力的花费+人均储蓄中用于替换旧资本的花费）。于是，我们就回答了上面留下的问题。更进一步，将这一关系式变形，可得：。此式说明：一个社会的人均储蓄可以分为两个部分：⑴现有技术装备水平下的人均资本的增加△k，即为每一个人配备更多的资本设备，这被称为资本的深化。⑵每一增加的人口配备每人平均应得的资本设备（n+δ）k，这被称为资本的广化。总而言之，这里的意思是：在一个社会全部产品中减去被消费掉的部分之后，剩下来的便是储蓄；在投资等于储蓄的均衡条件下，整个社会的储蓄可以被用于两个方面：一方面给每个人增添更多的资本设备，即资本深化，另一方面为新出生的每一个人提供平均数量的资本设备，即资本广化。只有等式 出现，一个社会的经济才会出现超速增长，而当△k=0时，则经济处于一种稳定的状态。

三、稳态分析

稳态是指一种长期稳定、均衡的状态，是人均资本与人均产量达到均衡数值并维持在均衡水平不变的一种状态。根据均衡的定义，均衡是对立的、变动着的经济变量处于一种力量相当、相对静止、不再变动的境界。如果均衡存在，应该有：

 

即，因此，稳态条件是。

可以用图形来分析稳态，如图7-2所示。

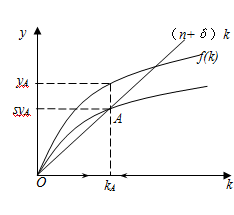⑴图7-2中，由于边际报酬递减规律的作用，人均生产函数曲线f(k)是一条向右上方倾斜且逐渐平缓的曲线。

⑵由于0＜s＜1，故储蓄曲线sf(k)与人均生产函数曲线f(k)的形状相同；又由于sf(k)＜f(k)，所以储蓄曲线sf(k)位于人均生产函数曲线f(k)下方。

⑶由于n、δ都为常量，故资本广化曲线(n+δ)k是通过原点、向右上方倾斜的直线。

⑷由于sy=（n+δ）k是稳态条件，所以，稳态时，sf(k)曲线与（n+δ）k曲线一定相交，交点是A点，对应的人均资本为kA，人均产量为yA，人均储蓄量为syA，此时，syA=（n+δ）kA，即人均储蓄正好能够全部用来为不断增长的劳动力购买资本品（花费为nkA）和替换旧的资本品（花费为δkA），人均资本没有变化（即△k =0）。

⑸从图7-2中可以看到，在A点之左，sf(k)曲线高于（n+δ）k曲线，表明人均储蓄大于资本广化，存在着资本深化即△k＞0。这时，人均资本k有增多的趋势，人均资本k会逐步地增加，逐渐接近于kA。当k的数量为kA即k=kA时，经济实现稳定状态。在A点之右，人均储蓄小于资本广化，即sf(k)＜（n+δ）k，此时有△k＜0，人均资本k有下降趋势。人均资本k的下降会一直持续到kA的数量上，达到稳态。

⑹以上论述表明，当经济偏离稳定状态时，无论是人均资本过多还是过少，经济都会在市场力量的作用下恢复到长期、稳定、均衡状态。

⑺从图形还可以看到，k值越小（意味着资本越贫乏），越有可能资本深化，故经济增长中穷国会快于富国；s值越高（意味着一国越富裕），sf(k)曲线越向上移动，从而使人均资本和人均产量提得越高；人口增长率n降得越低（意味着一国人口生育控制工作做得越好），可使（n+δ）k曲线向右下方转动，从而使人均资本和人均产量提高；通过调整k也可以使人均产量f(k)变动。

(8)稳态时，由于，，则资本的增长率为n，由于规模报酬不变，则总产量的增长率也为n。另外，也可以推导出人均资本增长率和人均产出增长率均为0。

四、稳态的变化

1.储蓄率的提高对稳态的影响。储蓄率的提高增加了稳态的人均资本量。新的稳态均衡时的人均收入大于旧稳态均衡时的人均收入。因此，储蓄率的提高还增加了人均收入。另外，这里所提到的稳态变化不是指由稳态到非稳态，而是指旧的稳态变化到新的稳态，经济变化前后都是稳态。这就是说，储蓄率的提高不能影响稳态增长率n，但能提高稳态的人均资本与人均收入水平。

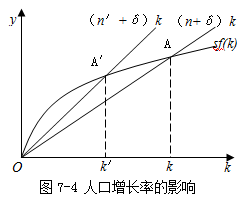
2.人口增长率提高对稳态的影响。以上分析的都是经济按照不变的劳动力增长率n来增长，现在就来分析把n看作是参数时，人口增长率提高对稳态产生的影响。从图中可以看到：人口增长率的增长降低了人均资本的稳态水平，人均资本由k降低到k′。又由于sf(k)曲线的上方有一条人均收入曲线，所以，新稳态均衡时的人均收入显然低于旧稳态均衡时的人均收入。因此，人口增长率的提高又减少了人均收入，即降低了人均产量的稳态水平；但是人口增长率的增长增加了总产量的稳态水平。这一结论揭示了发展中国家人均产量下降由人口增长率上升引起的现象，并且两个储蓄率相同的国家，人均收入会由于人口增长率不同而不同。

五、考虑到技术进步的索洛经济增长模型

（一）基本方程

前面关于新古典增长理论是在没有考虑技术进步情况下进行的。现把技术进步这一因素引入。需要注意的是技术进步（ ）在生产函数中的作用是：增加劳动要素（ ）的边际产量，或者增加资本要素（ ）的边际产量，或者同时提高资本和劳动要素的边际产量。技术进步不能脱离劳动和资本独立存在，因此，考虑到技术进步后 和 、 和 以相乘形式进入。如果技术进步进入的形式为 ，则此技术进步为劳动增进型或哈罗德中性；如果技术进步进入的形式为 ，则此技术进步为资本增进型；如果技术进步进入的形式为 ，则此技术进步为希克斯中性。我们以哈罗德中性的公式为例，即

                              （7.14）

式中AN被称为有效劳动。

（7.14）式两边同乘以λ，有。又设，则有。

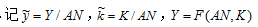
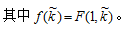
假设技术进步率为g，人口增长率为n，折旧率为δ。

 

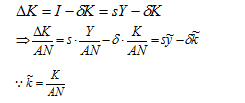
 　　　　              　（7.15）

                      （7.16）　

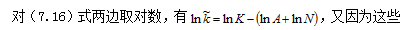
又因为这些变量都是时间t的变量，即

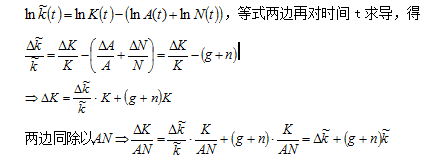 (7.17) 

联立（7.15）和（7.17），有

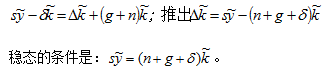
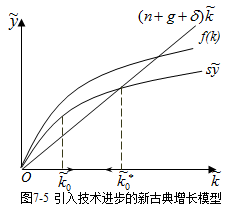
图7-5给出了引入技术进步的新古典增长模型的稳态分析图。

（二）基本结论

从图形及其文字分析中可以得出以下几点认识：

⑴引入技术进步并没有使稳态分析的结论产生大的波动；

⑷人均产出增长率只取决于技术进步速度。由于，，推出，对此式两边取自然对数，有，等式两边再对时间t求导，可得。从上一点可知道，k的增长率为零，故有人均产出y的增长率只取决于技术进步A的速度。

⑸总产出的增长速度取决于（）。因为，对此式两边取自然对数，有，等式两边再对时间t求导，可得。