安全多方计算协议
安全多方计算是解决在无可信第三方的情况下,互不信任的两个或多个用户,在不泄露各自私有输入信息的前提下,如何安全地协同合作,执行某个约定函数的计算问题。
安全多方计算是现代密码学的重要基础之一,在电子选举、门限签名、电子拍卖、秘密共享等领域得到了广泛应用。
安全多方计算基础协议包括不经意传输协议、秘密比较协议、置换协议、点积协议等。
秘密比较协议
姚期智老师的题设:
先简化问题,假设富翁A和B分别有i,j亿资产,其中i,j ∈ [1, 100]
B 拥有一对密钥(kEB, kDB),其中 kEB 为公钥,kDB 为私钥。A 知道 B 的公钥 kEB。
姚期智老师的算法:
<1> A 选择一个随机大整数 x,并使用 B 的公钥加密得到 c=EkEB(x);A 计算 c–i,并将结果发送给 B。
<2> B 计算以下 100 个数:yu=DkDB(c–i+w),u∈[1, 100]。B 需要选择略小于 x 的一个大素数 p(B 并不知道 x,但 A 可以将 x 的数量级告诉 B),然后计算以下 100 个数:Zu=yu mod p,u ∈[1, 100]。然后验证对所有的 u≠v, Zu –Zv ≥2,并对全部的 u 来验证 0<Zu<p–1。
<3> B 将以下数列依次发送给 A:Z1,Z2,…,Zj,Zj+1,…,Z100+1,p。
<4> A 验证上述数列的第 i 个数是否与 x mod p 同余。若同余,则 B 可得 i≤j,否则 i>j。
<5> A 将此结论告知 B。
该算法的简易描述:
第一步,经过特定的操作,让A构造出 n 个锁,B有且仅有第 j 个锁的钥匙,但是A不知道 j 是多少;
第二步,A给B n 个锁着的标志位,其中前 i 个标志位置0,后 n-i 个置1;
第三步,B检查第 j 个锁锁着的标志位是否为0。如果为0则 i >= j,否则 i < j。
不经意传输协议
不经意传输协议(Oblivious Transfer Protocol,OTP)又称为茫然传输协议,是由美国哈佛大学 M. Rabin 等人于 1981 年首次提出的。作为安全多方计算领域中极为重要的基础协议,一般模型下的安全多方计算问题理论上均可通过不经意传输协议来求解。
该协议实现了发送方将潜在的许多信息中的一个传递给接收方,但对接收方所接收信息保持未知状态。
在Rabin的协议基础上,不经意传输协议发展为二选一不经意传输(OT12)、n 选一不经意传输(OT1n)、 n 选 m 不经意传输(OTmn)等类型。
举例

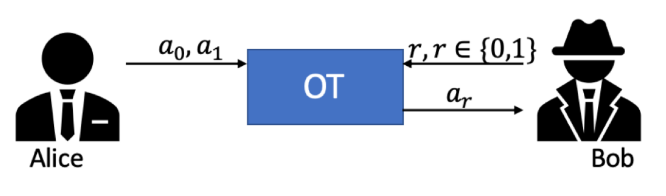
上图就是一个典型的OT12协议。
Alice每次发两条信息(a1、a2)给Bob,
Bob提供一个输入,并根据输入获得输出信息,
在协议结束后,Bob得到了自己想要的那条信息(a1或者a2),而Alice并不知道Bob最终得到的是哪条。
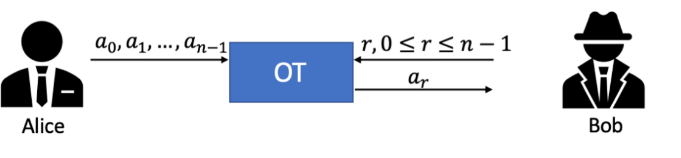
上图就是一个典型的OTn1协议。
Alice每次发n条信息(a0、a1、… , an-1)给Bob,
Bob提供一个输入,并根据输入获得输出信息,
在协议结束后,Bob得到了自己想要的那条信息(ai),而Alice并不知道Bob最终得到的是哪条。
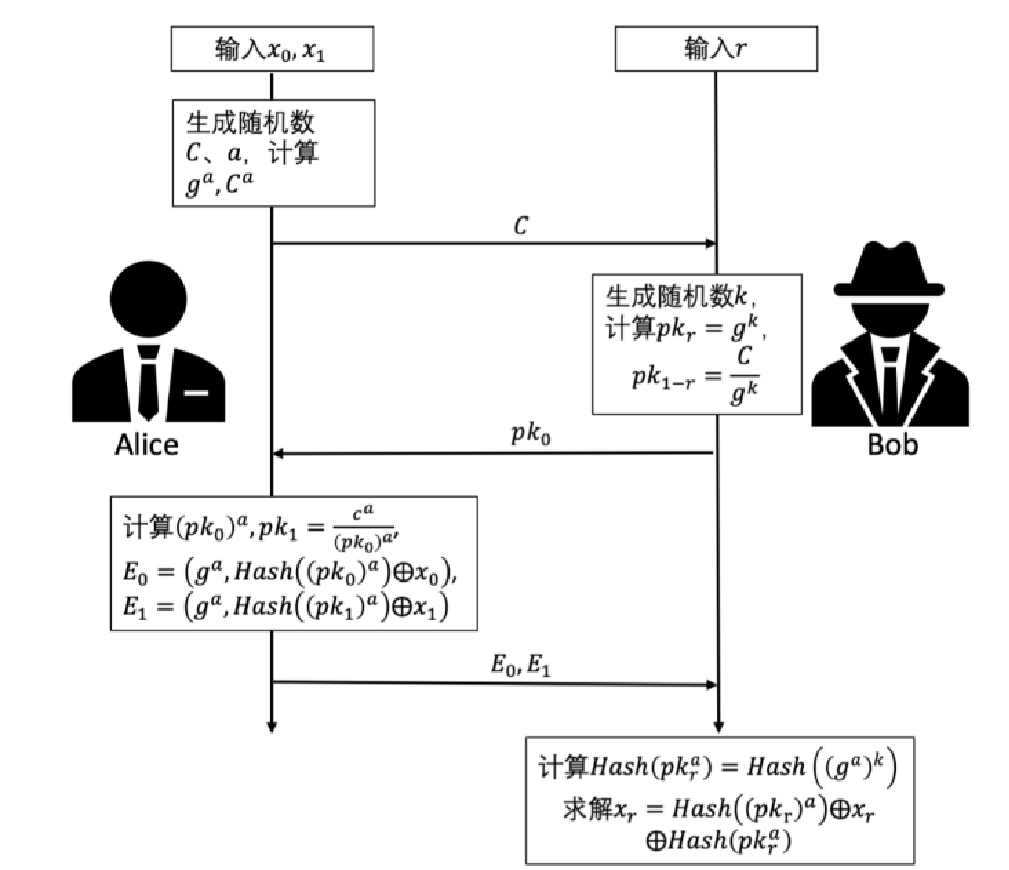
Naor-Pinkas不经意传输协议是经典的OT协议,其基于离散对数困难问题,通过三次公钥密码学操作实现了 OT12.
安全置换协议
安全多方置换问题可以描述为:
A 拥有一个 n 维私密向量 X=(x1, x2, …, xn),
B 拥有一个置换排列函数π和 n 维私密向量 Y=(y1, y2, …, yn),B 向 A 公开π,二者合作计算π(X+Y),A 需要获得π(X+Y),同时要求 A 不能获得 Y 和任何 yi,i∈[1, N]的信息,B 也不能获得任何 xi 的信息。
保密点积协议
保密点积协议是许多安全多方计算问题中一个重要的协议,常被用在许多保密数据挖掘协议中,为这些协议提供了重要的安全保证。该协议潜在的应用领域是广阔的,如计算欧几里得距离、保密计算几何、保密协作统计分析等。
保密点积协议 (privacy-preserving dot product protocol). 该问题最初被 Du 和 Atallah 在2001年提出。协议可描述为:
假设有两个参与者,
Alice 拥有秘密输入向量X=(x1, … xn) ,
Bob 拥有秘密输入向量 Y=(y1, …, yn),
他们希望进行合作计算并在协议结束后, Alice 得到值rA = X ⋅ Y - rB(这里 rB 是 Bob 选取的一个随机值).
同时要满足 Alice 不能从 rA中得到有关 X ⋅Y 的值, 也不能从自己获取的信息中推出任何有关 yi的信息; Bob 不能得到 rA的值, 也不能推出有关 xi 的信息.
点积协议可以采用不经意传输等方式来构建。


