利用力系简化的方法，可以求得平面任意力系的合力。

2

讨论2:同向分布平行力系的合成 

图2.27所示为作用在梁上的同向分布平行力系。载荷（力）的分布集度（单位长度上作用的力）为q(x), 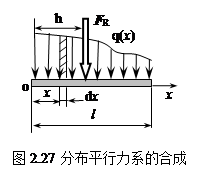量纲为［力/长度］，如N/m或kN/m。

为求同向分布平行力系的合力，在距o点x处取微段dx，作用在该微段上的力为 q(x)dx。以o点为简化中心，将各微段上的力均平移至o点，得到：

主矢：F_R′=∑q(x)dx=  

主矩为：Mo=∑xq(x)dx=   

因为主矢F_R′≠0，且主矩Mo≠0；故同向分布平行力系可合成为一个合力F_R，且合力F_R的大小为：

F_R= F_R′ =                                ----(2-12)

(2-12)式表示合力F_R的大小等于分布载荷图形的面积。

合力F_R的作用线到o点的距离为：

 h=Mo/F_R′ =                   ----(2-13)

(2-13)式是分布载荷图形的形心公式，故合力F_R的作用线通过分布载荷图形的形心。

    因此，同向分布平行力系可合成为一个合力，合力的大小等于分布载荷图形的面积，作用线通过图形的形心，指向与原力系相同。

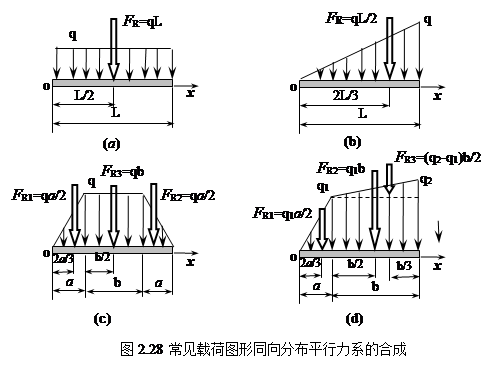
图2.28 给出了几种常见同向分布平行力系的合成结果。图2.28(a)是均匀分布载荷，其合力在数值上等于载荷图形（矩形）的面积（q×L），作用线通过载荷图形的形心，距二端为L/2。图2.28(b)是线性分布载荷，其合力在数值上等于载荷图形（三角形）的面积 [(q×L)/2]，作用线通过载荷图形的形心，即距右端为L/3。分布力系图形复杂时，可以先分成若干部分，各部分分别合成，如图2.28（c）和2.28（d），再求其最终的合力。