两类特殊函数:匿名函数,递归函数

下面介绍 递归函数

【例】 计算4的阶乘。

两种方法：

方法一：通过循环语句来计算阶乘,该方法的前提是了解阶乘的计算过程,并可用语句把计算过程模拟出来。

方法二通过递推关系将原来的问题缩小成一个规模更小的同类问题,将4的阶乘问题转换为3的阶乘问题,只需找到4的阶乘和3的阶乘之间的递推关系,以此类推,直到在某一规模上(当n 为1时)问题的解已知,其后,回归。这种解决问题的思想称为递归。

方法一：循环

s =1

for i in range(1,4):

   s =s * i

print(s)

方法二：递归

def fac(n):

   if n==1:

      return 1

    return n * fac(n -1)

fac(4)  

递归求解过程: 递归调用的过程类似于多个函数的嵌套调用,只不过这时的调用函数和被调用函数是同一个函数,即在同一个函数中进行嵌套调用。

    递归是通过“栈”来实现的,按照“后调用先返回”的原则———每当函数调用时,就在栈顶

分配一个存储区;每当退出函数时,就在栈顶释放该存储区。

【例】编写计算n!的函数。

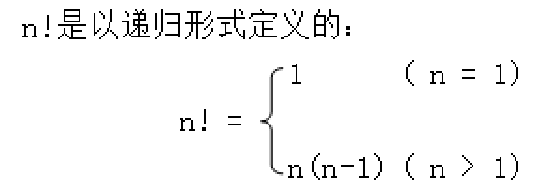
  计算n!，应先计算(n - 1)!，而计算(n - 1)!，需要先计算(n - 2)!， ......，如此递推，直到最后变成计算1!的问题。

  根据公式，1! = 1，这是本问题的递归终止条件。由终止条件得到1!的结果后，再反来依次计算出2!，3!，......，直到最后计算出n!。

 设计算n!的函数为fun(n)，当n>1时，fun(n) = n * fun(n-1)。即在fun(n)函数体内将递归调用fun()自身。