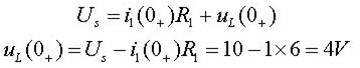初始值计算步骤：

a.根据换路定律求 uc(0+)、iL(0+) ；

b.画 t=0+时刻的电路图；

c.根据ＫＶＬ、ＫＣＬ及欧姆定律求其他初始值。  

注意:画t=0+时刻电路图时，若uc(0+)=0，则此时电容元件相当于短路；若uc(0+)≠0, 此时电容元件相当于电压为uc(0+)的电压源。若iL(0+)=0，则此时电感元件相当于开路；若iL(0+) ≠0,则此时电感元件相当于电流为 iL(0+)的电流源。

例题7-1:

如图7-1（a）所示电路中, 已知Us=12V，R1=4kΩ，R2=8kΩ，C=1μF, 开关S原来处于断开状态, 电容上电压uc(0-)=0。求开关S闭合后，t=0+时, 各电流及电容电压的数值。 

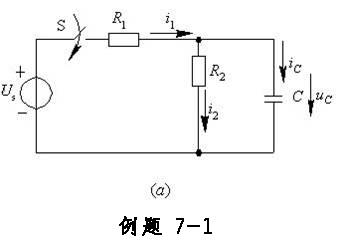
解：选定关联参考方向如图所示。

(1) 由已知条件可知: uc(0-)=0

(2) 由换路定律可知:

(3) 求其它各电流、电压的初始值。画出 t=0+时刻的等效电路, 如图7-1（b）所示。由于uc(0+)=0 , 所以在等效电路中电容相当于短路。故有

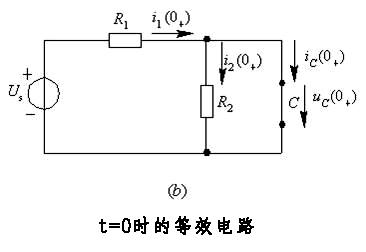
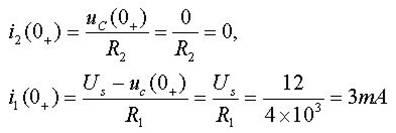
由KCL有

例题7-2

如图7-2（a）所示电路, 已知Us=10V, R1=6Ω, R2=4Ω, L=2mH, 开关S原处于断开状态。求开关S闭合后t=0+时, 各电流及电感电压uL的数值。

解：选定关参考方向如图所示。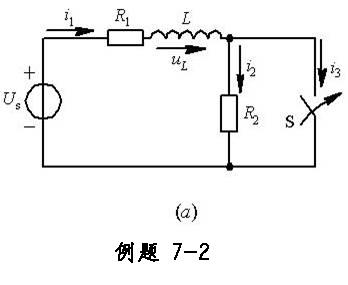

（1）求t=0- 时电感电流 iL(0-)。

由原电路已知条件得

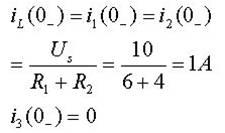
（2）求t=0+ 时iL(0+) 。由换路定律知

（3）求其它各电压、电流的初始值。画出t=0+时的等效电路如图7-2（b）所示。由于S闭合, R2被短路, 则R2两端电压为零, 故i2(0+)=0。

由KCL有：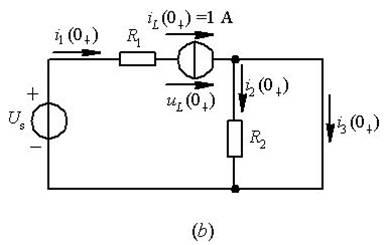

由KVL有：