串联谐振的条件和特征
RLC串联电路如图4-37所示,图4-38是其相量图。
其等效复阻抗为

阻抗角(即电压与电流的相位差)为
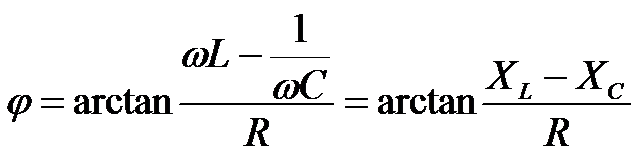
因而产生串联谐振的条件是φ=0,即

发生谐振的角频率称为谐振角频率,以![]() 表示。
表示。
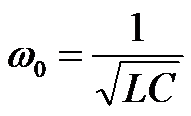
谐振频率

可见,当电路参数L和C为一定值时,电路产生的谐振频率就为一定值,与电阻R无关。所以,它反映了电路的一种固有性质,因此又称![]() 为谐振电路的固有频率,
为谐振电路的固有频率,![]() 为谐振电路的固有角频率。
为谐振电路的固有角频率。
综上,串联谐振电路的特征为:
(1) Z=R,阻抗Z=R最小,电路呈电阻性质。
(2) 电流具有最大值Io=U/R。
(3)谐振时电感与电容两端的电压大小相等,相位相反,电阻上的电压等于电源电压。
(4)总无功功率等于零。
特性阻抗和品质因数
(1) 特性阻抗
谐振时,电路的电抗为零,但感抗与容抗不为零,此时的感抗或容抗称为谐振电路的特性阻抗,用ρ表示,即
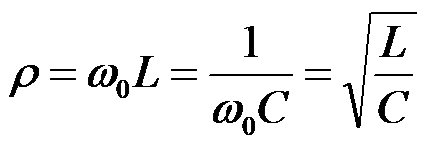
ρ的单位为欧姆(Ω),它是由电路的L、C参数决定的。
(2) 品质因数
谐振电路的特性阻抗P与电路中电阻R的比值大小来表征谐振电路的性能,此比值称为电路的品质因数,用字母Q表示。即
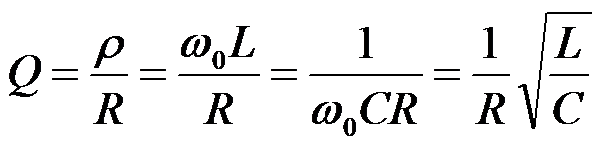
品质因数Q是一个无单位的物理量,其大小由电路中R、L、C的数值决定。这样,谐振时电感和电容的电压有效值为
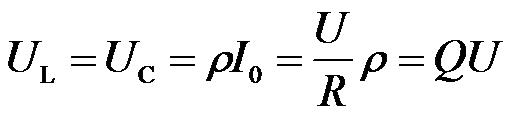
由上式可知,电路发生串联谐振时,电感电压和电容电压大小是电源电压的Q倍。当品质因数Q很大时,电感电压和电容电压就可能远大于电源电压,所以串联谐振又称为电压谐振。在实际电路中,串联谐振的发生会使电压过高可能会击穿线圈或电容的绝缘,因此在电力工程中应避免发生谐振,防止过高电压的产生而造成危害。但在无线电工程中常利用串联谐振以获得较高电压来提取微弱信号。
谐振曲线

当电压一定,电流I随频率变化的关系曲线称为谐振曲线。在RLC串联电路中电流为
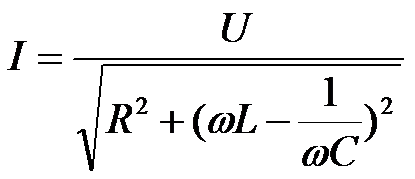
从串联谐振曲线可知,当![]() 时,电流达到最大值,即谐振电流
时,电流达到最大值,即谐振电流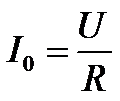 。电流在
。电流在![]() 附近的一段频率内,电流有较大的幅值。当ω逐渐远离
附近的一段频率内,电流有较大的幅值。当ω逐渐远离![]() 时,电流则逐渐减小,说明电路对电流的抑制力逐渐增强。通常把谐振曲线上电流为
时,电流则逐渐减小,说明电路对电流的抑制力逐渐增强。通常把谐振曲线上电流为![]() 所对应的两个频率之间的宽度(频率范围)称为通频带,简称带宽。通频带用
所对应的两个频率之间的宽度(频率范围)称为通频带,简称带宽。通频带用![]() 表示,即
表示,即![]() 。式中,
。式中,![]() 、
、![]() 是通频带低端和高端频率。可以证明
是通频带低端和高端频率。可以证明
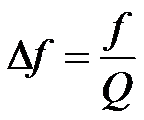
可以看出,串联谐振电路具有“选频”的本领,频率在通频带内的信号容易通过RLC串联电路,而频率在通频带外的信号则很难通过电路。这种能够选择出谐振角频率![]() 及其附近频率所对应电流的性能称为电路的选频特性,即选择性。
及其附近频率所对应电流的性能称为电路的选频特性,即选择性。

若以![]() 为横坐标,以
为横坐标,以![]() 为纵坐标,根据式(4-65)可以作出取不同Q值时的谐振曲线。
为纵坐标,根据式(4-65)可以作出取不同Q值时的谐振曲线。
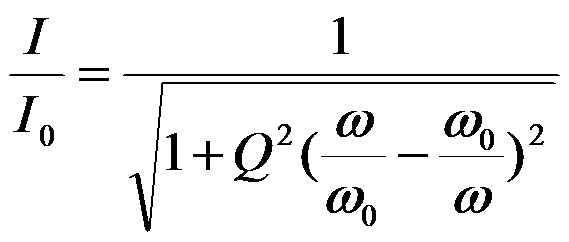
由分析可知,电路的选择性好,通频带就窄;反之,通频带越宽,选择性就越差。所以在无线电技术中,合理地选择品质因数的大小,以充分兼顾通频带和选择性。


