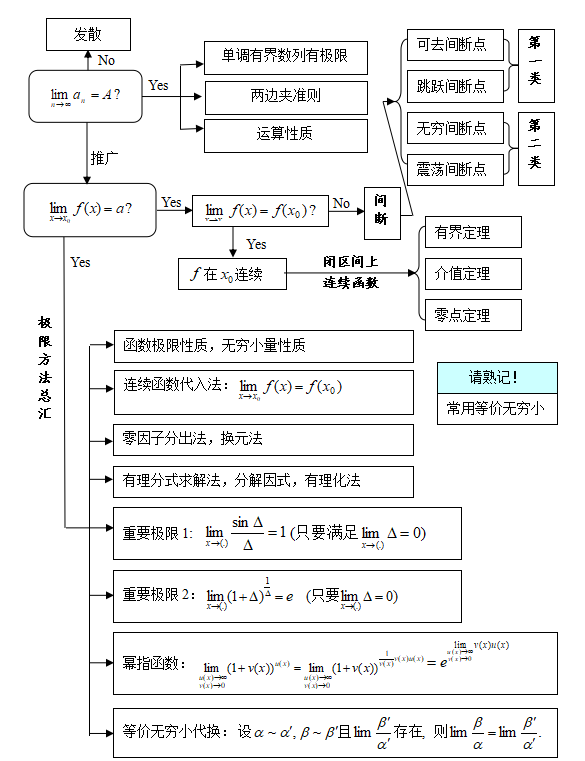
本章首先给出了数列极限、函数极限的概念,并不加证明地给出数列极限和函数极限的性质。重点介绍了计算极限的一些经典方法,函数连续的概念、函数间断点的类型及闭区间上连续函数的性质。通过完成本章达标实训练习,可使读者达到以下要求。
一级达标要求:掌握应用极限的运算法则求极限的方法,理解无穷小、无穷大、以及无穷小的阶的概念。理解极限存在的两边夹定理,了解单调有界数列必有极限的原理,会用两个重要极限求极限,熟练应用型的简便算法及等价无穷小代换求极限。理解函数在一点连续和在一个区间上连续的概念,了解间断点的概念,并会判别间断点的类型。了解初等函数的连续性和闭区间上连续函数的性质(介值定理,最大最小值定理,零点定理)。
二级达标要求:在一级达标要求的基础上,熟练掌握计算极限的经典方法,并会解决一些复杂综合性的求极限的问题,判断复杂函数的间断点类型,了解应用极限和连续解决实际问题的方法。
2024年考研数学一大纲
考研考试形式和试卷结构
一、试卷满分及考试时间
试卷满分为150分,考试时间为180分钟.
二、答题方式
答题方式为闭卷、笔试.
三、考试内容
高等数学60%、线性代数20%、概率论与数理统计20%
四、试卷题型结构
单项选择题选题10小题,每题5分,共50分
填空题6小题,每题5分,共30分
解答题(包括证明题)7小题,共70分
【数一】函数、极限、连续
函数的概念及表示法、函数的有界性、单调性、周期性和奇偶性、复合函数、反函数、分段函数和隐函数、基本初等函数的性质及其图形、初等函数、函数关系的建立;数列极限与函数极限的定义及其性质、函数的左极限和右极限、无穷小量和无穷大量的概念及其关系、无穷小量的性质及无穷小量的比较、极限的四则运算、极限存在的两个准则;单调有界准则和夹逼准则、两个重要极限、函数连续的概念、函数间断点的类型、初等函数的连续性、闭区间上连续函数的性质.
考试要求
1.理解函数的概念,掌握函数的表示法,会建立应用问题的函数关系.
2.了解函数的有界性、单调性、周期性和奇偶性.
3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.
4.掌握基本初等函数的性质及其图形,了解初等函数的概念.
5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.
6.掌握极限的性质及四则运算法则.
7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极
限求极限的方法.
8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价
无穷小量求极限.
9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.
10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.
2024年考研数学二大纲
考试科目:高等数学、线性代数
考试形式和试卷结构
一、试卷满分及考试时间
试卷满分为150分,考试时间为180分钟.
二、答题方式
答题方式为闭卷、笔试.
三、考试内容
高等数学80%、线性代数20%
四、试卷题型结构
单项选择题选题10小题,每题5分,共50分
填空题6小题,每题5分,共30分
解答题(包括证明题)7小题,共70分
【数二】函数、极限、连续
函数的概念及表示法、函数的有界性、单调性、周期性和奇偶性、复合函数、反函数、分段函数和隐函数、基本初等函数的性质及其图形、初等函数函数关系的建立.
数列极限与函数极限的定义及其性质、函数的左极限与右极限、无穷小量和无穷大量的概念及其关系、无穷小量的性质及无穷小量的比较、极限的四则运算、极限存在的两个准则:单调有界准则和夹逼准则、两个重要极限、函数连续的概念、函数间断点的类型、初等函数的连续性、闭区间上连续函数的性质.
考试要求
1.理解函数的概念,掌握函数的表示法,并会建立应用问题的函数关系.
2.了解函数的有界性、单调性、周期性和奇偶性.
3.理解复合函数及分段函数的概念、了解反函数及隐函数的概念、掌握基本初等函数的性质及其图形、了解初等函数的概念、理解极限的概念、理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.
4.掌握极限的性质及四则运算法则.
5.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.
6.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.
7.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.
8.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.
中国古代极限思想
早在春秋战国时期(公元前770——前221),古人就对极限有了思考。道家的庄子在《庄子》“天下篇”中记载:“一尺之捶,日取其半,万世不竭”。意思是说,把一尺长的木棒,每天取下前一天所剩的一半,如此下去,永远也取不完。也就是说,剩余部分会逐渐趋于零,但是永远不会是零。而墨家有不同的观点,提出一个“非半”的命题,墨子说“非半弗,则不动,说在端”。意思是说将一线段按一半一半地无限分割下去,就必将出现一个不能再分割的“非半”,这个“非半”就是点。道家是“无限分割”的思想,而墨家则是无限分割最后会达到一个“不可分”的思想。
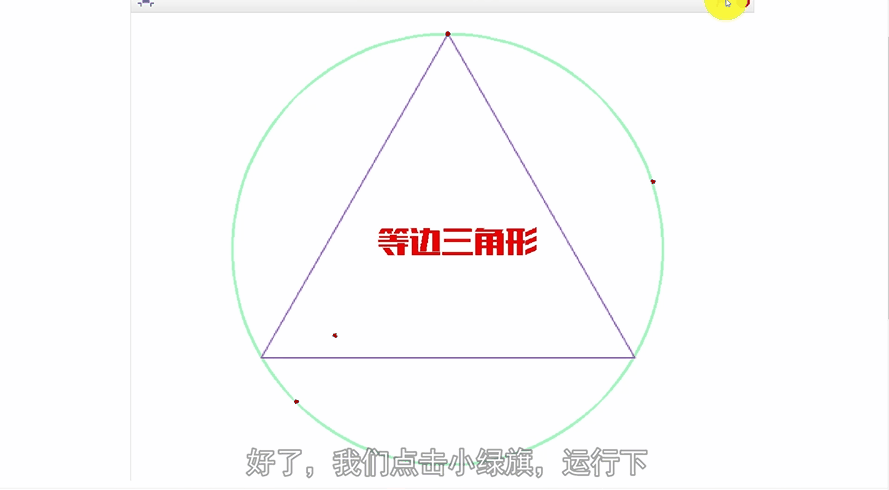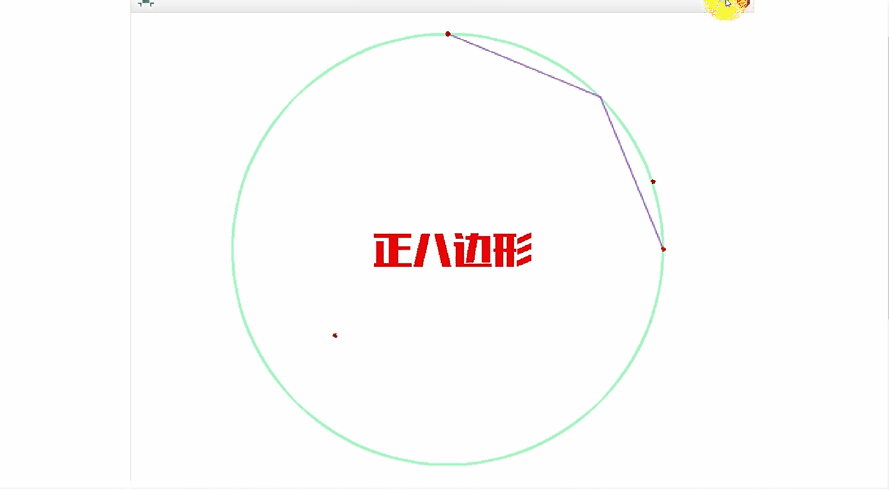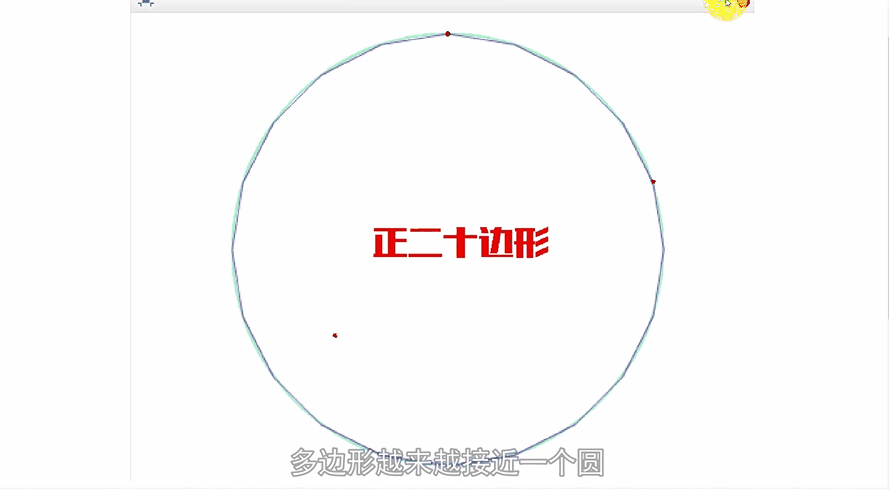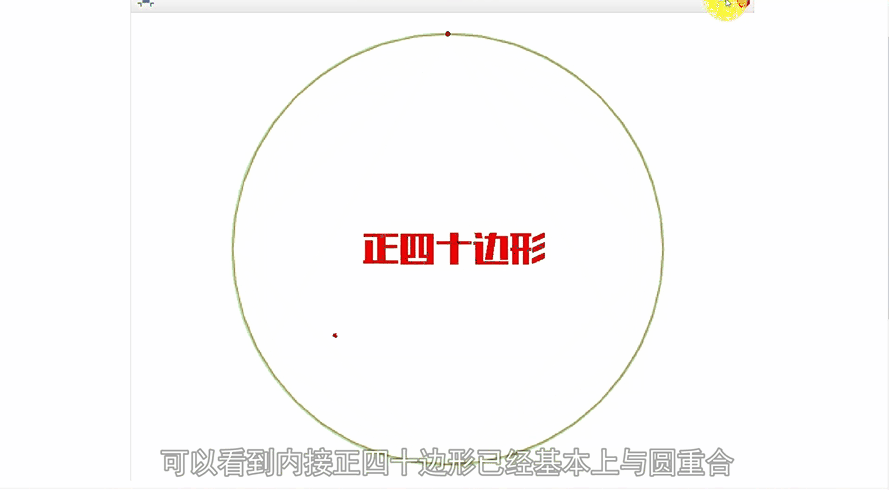
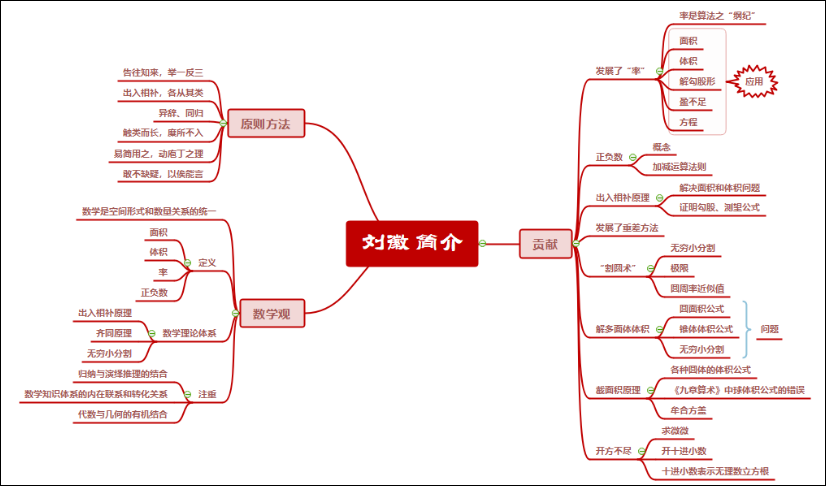
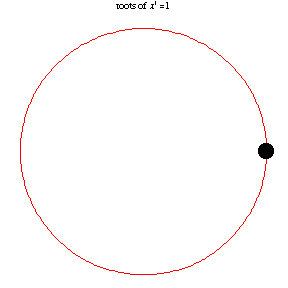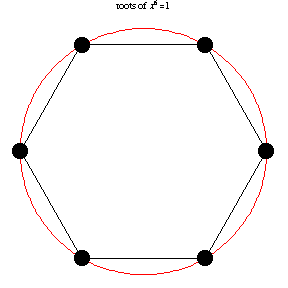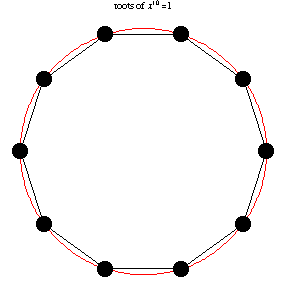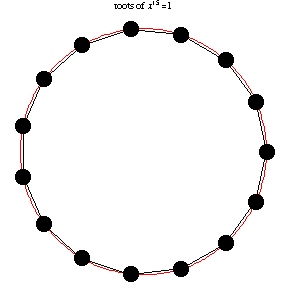
公元3世纪,我国魏晋时期的数学家刘徽在注释《九章算术》时创立了有名的“割圆术”,他创造性地将极限思想应用到数学领域。他设圆的半径为一尺,从圆内接正六边形开始,每次把边数加倍,用勾股定理算得圆内接正十二、二十四、四十八…边形的面积,内接正多边形的边数越多,内接多边形的面积就与圆面积越接近,正如刘徽所说:“割之弥细,所失弥少,割之又割,以至不可割,则与圆周合体,而无所失矣”。这已经运用了极限论的思想来解决求圆周率的实际问题了,“以至不可割,则与圆周合体”,这一思想是墨家“不可分”思想的实际应用。
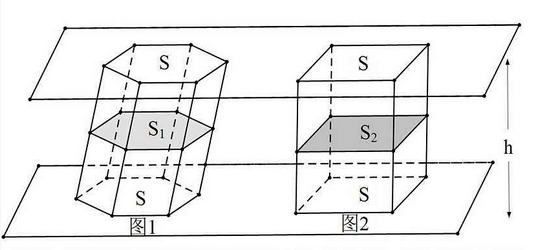
祖暅之《缀术》有云:“缘幂势既同,则积不容异。”祖暅沿用了刘徽的思想,利用刘徽“牟合方盖”的理论去进行体积计算,得出“幂势既同,则积不容异”的结论。意思是界于两个平行平面之间的两个立体,被任一平行于这两个平面的平面所截,如果两个截面的面积相等,则这两个立体的体积相等。这正是“不可分”思想的延续。
公元三世纪,古希脂诡辩学家安提丰(Antiphon,约公元前430年)在求圆面积时曾提出了用成倍扩大圆内接正多边形边数,通过内接正多边形的面积来表示圆面积的方法,即“穷竭法”。他先作圆内接正方形,然后将边数加倍,得到圆内接正八边形,再加倍得内接正十六边形,依次继续下去,以为这样圆与内接正多边形的差将被“穷竭”。这是一种粗糙的极限论思想,虽然获得的结果是正确的,但在逻辑上是有问题的,谁能保证无限扩大后的正边形的边与圆周会重合呢?这就是所谓的希腊数学家的“关于无限的困惑”。这种边数加倍的过程可以无限制地进行,不会有所终结,因而“差”被“穷竭”的说法是不合适的。
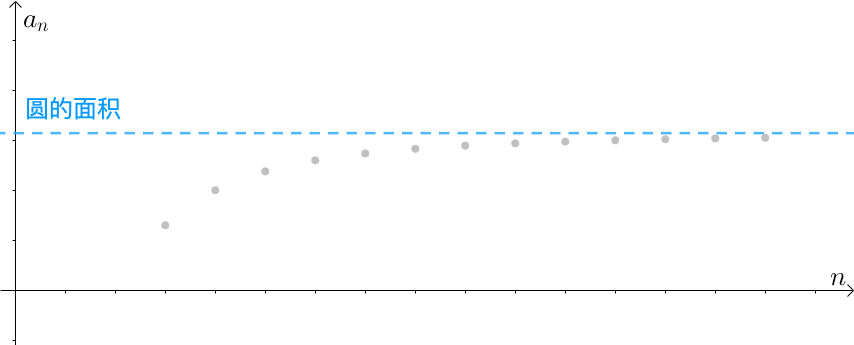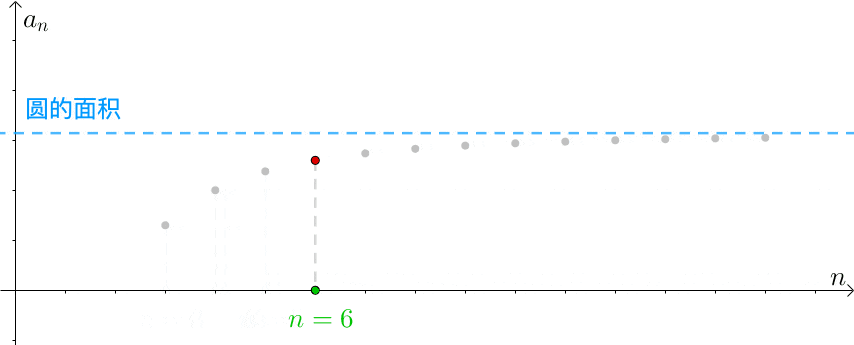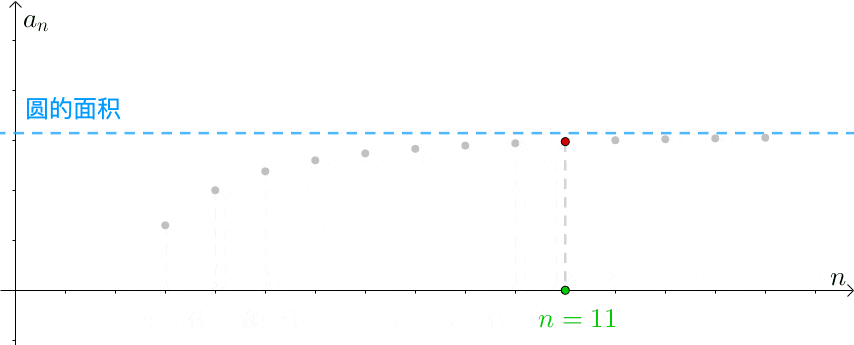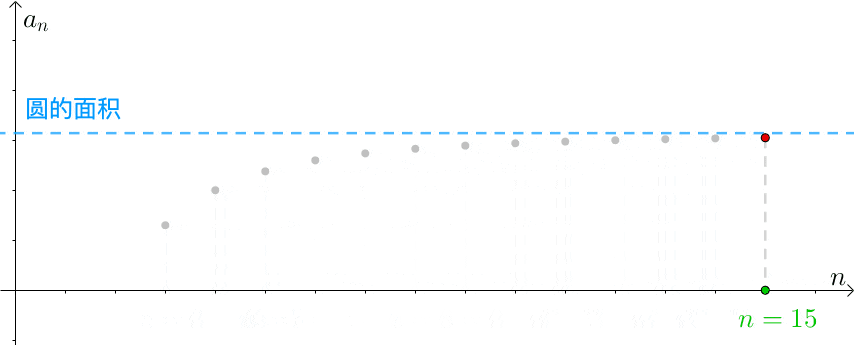
欧多克索斯建立了严谨的穷竭法,并用它证明了一些重要的求积定理。穷竭法的逻辑依据,是欧多克索斯推得的下述结果:“设给定两个不相等的量,如果从其中较大的量减去比它的一半大的量,再从所余的量减去比这余量的一半大的量,继续重复这一过程,必有某个余量将小于给定的较小的量”。这个结果,现在被称为欧多克索斯原理。欧多克索斯的穷竭法可看做是微积分的第一步,但没有明确地用极限概念,也回避了“无穷小”概念。
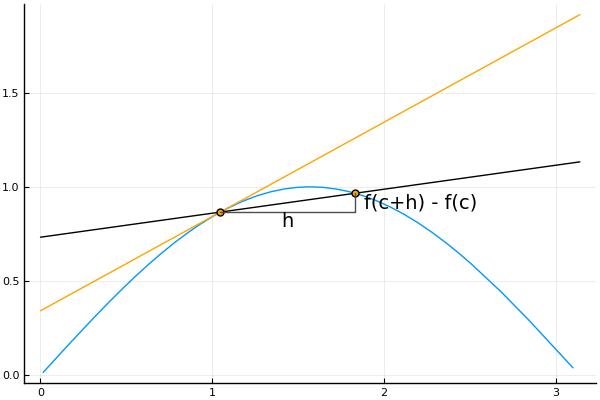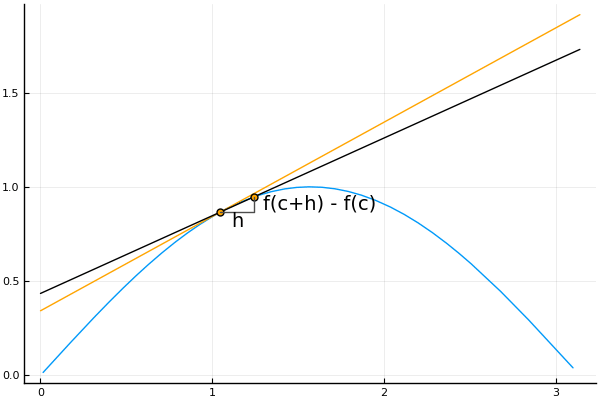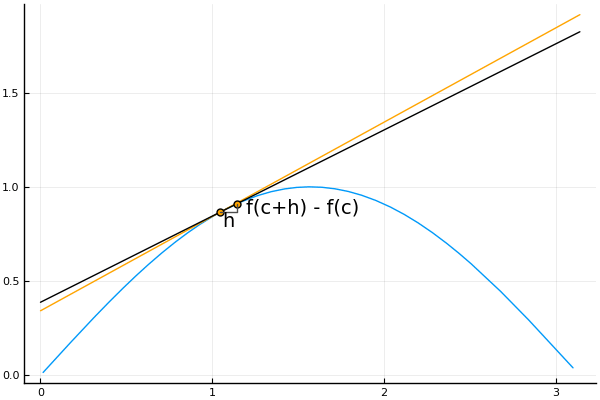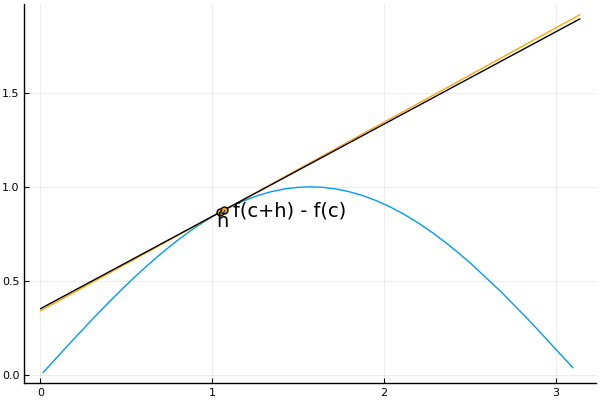
“穷竭法”后来由古希腊的大科学家阿基米德(Archimedes,公元前287-前212)加以改进。他在用“穷竭法”求抛物线的弓形面积时,发现这种方法似乎还不够严密,因此在获得结果后再用归谬法,从逻辑上证明了结果的正确性。他发现第n个多边形的面积与抛物线弓形面积有一个差值。由于随着n的增大,这个差值也将越来越小,直到不可能是一个确定的大于零的常数,但这个差值也不可能是小于零的,因此根据归谬法差值只可能等于零。
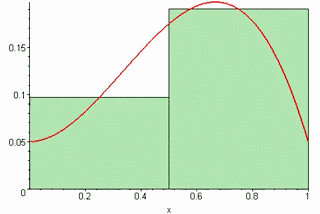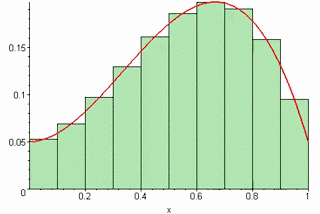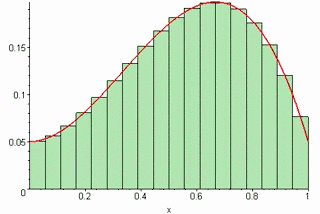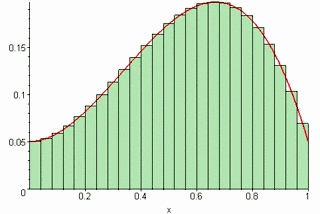
阿基米德在此提出了一个相当于现在无穷小量的概念。同时我们可以看到阿基米德所使用的归谬法正是柯西极限思想的雏形,也就是说现行极限思想只是阿基米德用来证明“穷竭法”结果的方法的思想,而对于分割的过程是没有体现的,也就是对于“不可分量”或“无限可分”思想没有做出解释。