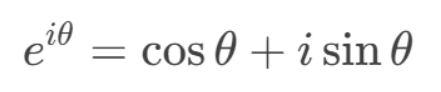从古至今,数学一直是人类探索世界、理解自然规律的重要工具。而在众多数学分支中,三角函数无疑是最具影响力和实用性的工具之一。它不仅是数学理论的核心组成部分,更是物理学、工程学、计算机科学等领域的基石。从古代的天文测量到现代的量子计算,三角函数跨越千年,始终在塑造着我们的世界。
三角函数的起源:从天文测量到几何学
三角函数的起源可以追溯到古代文明。早在公元前2000年,古巴比伦人就开始使用简单的三角学知识来测量土地和天文现象。然而,真正奠定三角函数基础的,是古希腊的数学家们。
希帕克斯:三角学的奠基者
公元前2世纪,古希腊天文学家希帕克斯(Hipparchus)被认为是三角学的奠基者。他为了研究天文学,编制了历史上第一张正弦表。这张表格帮助他计算太阳和月亮的运动轨迹,从而预测日食和月食。希帕克斯的工作为后来的数学家提供了重要的工具。
托勒密:三角学的集大成者
公元2世纪,古希腊数学家托勒密(Ptolemy)在其著作《天文学大成》中进一步发展了三角学。他提出了著名的“托勒密定理”,并完善了正弦表。托勒密的工作不仅推动了天文学的发展,也为三角函数的系统化奠定了基础。
三角函数的发展:从几何学到解析工具
随着数学的发展,三角函数逐渐从几何学中独立出来,成为一种强大的解析工具。这一过程中,印度和阿拉伯数学家发挥了重要作用。
首先是印度数学家的贡献。公元5世纪,印度数学家阿耶波多(Aryabhata)首次将正弦函数定义为半弦长与半径的比值,并引入了余弦函数的概念。他的工作使得三角函数的计算更加简便,为后来的数学发展铺平了道路。
再有阿拉伯数学家的传承。公元9世纪,阿拉伯数学家阿尔·花剌子密(Al-Khwarizmi)在其著作中系统整理了三角学知识,并将其传播到欧洲。阿拉伯数学家还发明了正切函数,进一步扩展了三角函数的应用范围。
再到文艺复兴时期的突破。文艺复兴时期,欧洲数学家开始将三角函数与代数相结合。法国数学家韦达(Vieta)首次将三角函数表示为无穷级数,而瑞士数学家欧拉(Euler)则引入了复数和指数函数的概念,建立了著名的欧拉公式:
这一公式将三角函数与复数、指数函数联系起来,成为现代数学的重要基石。
三角函数的应用:从建筑到现代科技
三角函数的应用范围极其广泛,几乎渗透到现代社会的每一个角落。下面是几个典型的例子:
1. 建筑与工程
在古代,三角函数被广泛应用于建筑和工程领域。如,古埃及人利用三角学知识测量金字塔的高度,而古希腊人则用它设计帕特农神庙的完美比例。在现代,三角函数仍然是建筑设计和工程计算的核心工具。再如,工程师利用三角函数计算桥梁的受力分布,或者设计摩天大楼的结构稳定性。
2. 天文学与导航
三角函数在天文学和导航领域的应用可以追溯到古代。古希腊天文学家利用三角函数计算行星的轨道,而阿拉伯航海家则用它确定船只的位置。在现代,全球定位系统(GPS)仍然依赖于三角函数来计算卫星与地面接收器之间的距离。
三角函数的未来:从经典到量子
随着科技的进步,三角函数的应用范围还在不断扩大。在量子计算领域,三角函数被用于描述量子态的叠加和纠缠。在人工智能领域,傅里叶变换和三角函数被用于处理大规模数据。可以预见,三角函数将继续在未来的科技发展中发挥重要作用。
三角函数跨越千年,从古代的天文测量到现代的量子计算,始终在塑造着我们的世界。它不仅是一种数学工具,更是人类智慧的结晶。正如欧拉公式所揭示的那样,三角函数将数学的各个分支紧密联系在一起,展现出数学的和谐与美。无论你是学生、工程师还是科学家,学习和掌握三角函数都将为你打开一扇通往新世界的大门。让我们一起感受三角函数的魅力,探索数学的无限可能!
以上内容引自:《遇见数学》,仅供教学使用!!!