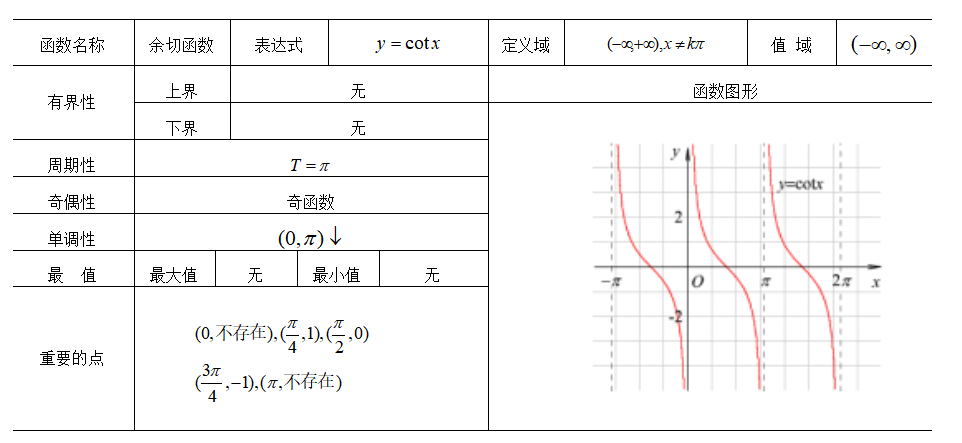
数学,作为理解世界的语言,隐藏着无数迷人的故事和实用的工具。在这个世界中,三角函数以其独特的魅力脱颖而出。想象一下,数千年前的古埃及,当时的建筑师和测量师面临着一个巨大的挑战:如何准确测量并重建尼罗河泛滥后被水冲刷掉的土地边界?他们可能没有现代的测量工具,但他们有三角函数——一个强大的数学工具,它能够帮助他们精确地测量和划分土地。这个故事不仅揭示了三角函数的实际用途,也映射出人类智慧的光辉。
三角函数的历史背景与故事
在三角函数的历史长河中,我们首先回到了古埃及和古希腊。古埃及的建筑师和测量师在建造金字塔和测量土地时,已经在使用三角学的原始形式。他们可能还没有明确地定义出我们今天所熟知的三角函数,但他们对角度和长度的关系有着深刻的认识。
随后,古希腊的天文学家和数学家开始更系统地研究三角学。喜帕恰斯被誉为三角学的奠基人。他通过将圆周分为360等份,并为指定弧度给出对应的弦长,为三角函数的发展奠定了基础。
三角函数的理论在印度和阿拉伯地区得到进一步的发展。印度天文学家Aryabhata在其著作中给出了完整的三角函数表述,这些表述更接近于我们现在所理解的正弦和余弦函数。阿拉伯学者花刺子密制作了正切表,进一步丰富了三角函数的体系。
这一时期的数学家不仅定义了三角函数,还制作了各类三角函数表,这些成就极大地促进了三角学的应用,特别是在天文学和测量学中。
最初,三角学的研究侧重于和弦——圆上两点间弧线的直线距离。然而,随着数学的发展,特别是在印度学者的贡献下,和弦的概念逐渐向我们现在所熟悉的正弦和余弦转变。这一转变不仅简化了计算,也使得三角函数更加易于在各种不同的场景中应用。
三角函数的定义与几何基础
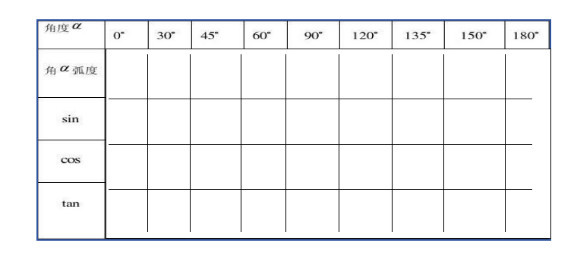
在直角三角形中,三角函数定义为边长之间的比例。包括:
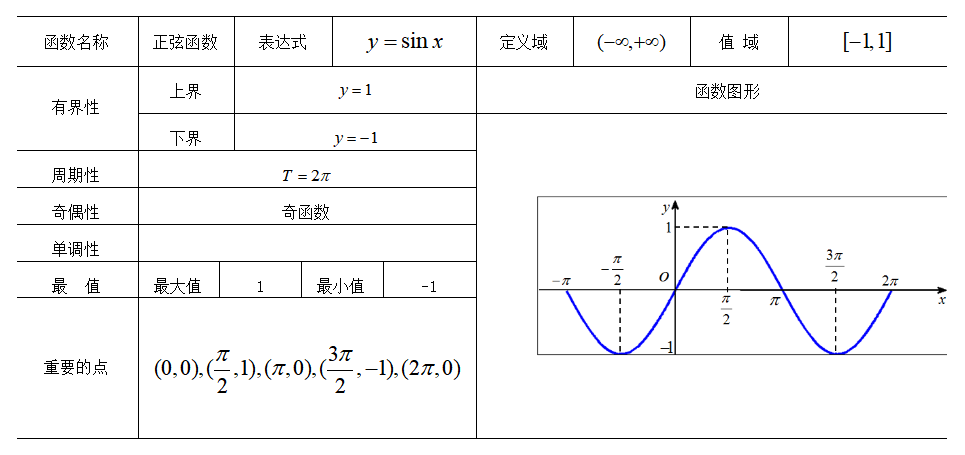
正弦函数(sine, sin):在直角三角形中,一个锐角的对边与斜边的比例。
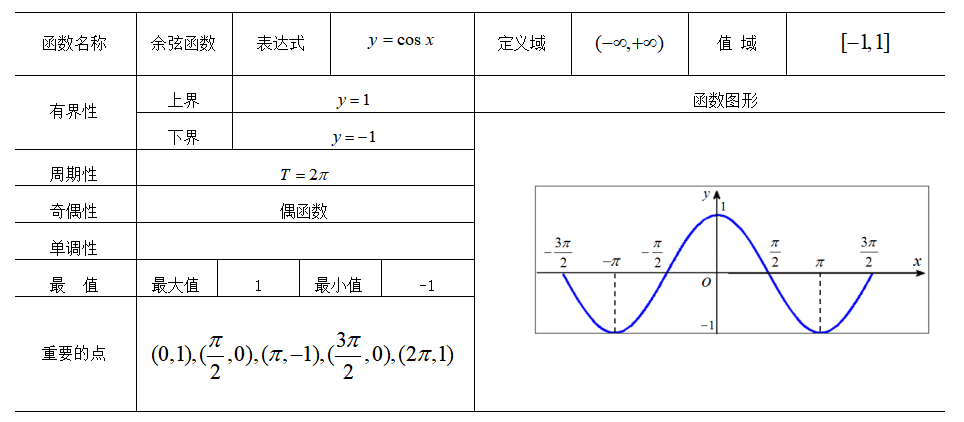
余弦函数(cosine, cos):直角三角形中,一个锐角的邻边与斜边的比例。
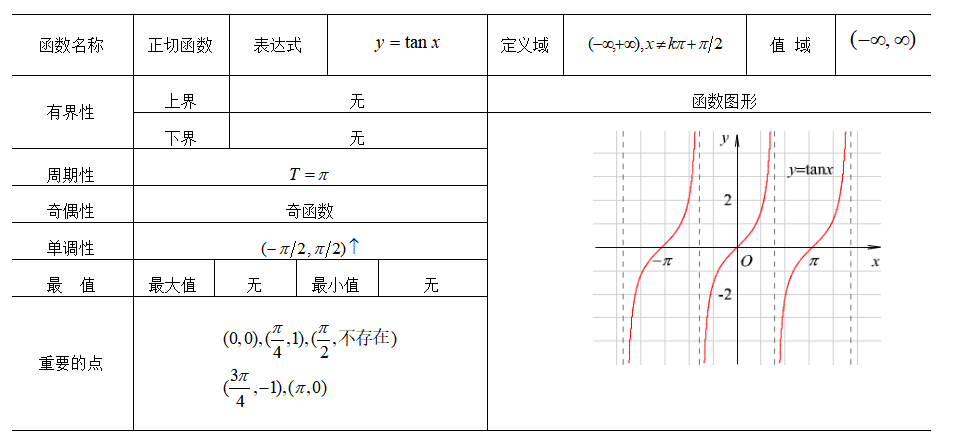
正切函数(tangent, tan):直角三角形中,一个锐角的对边与邻边的比例。
三角函数也可以通过单位圆(半径为1的圆)来理解。在这种情况下,一个角度对应于单位圆上一点的坐标:
正弦是该点的y坐标。
余弦是该点的x坐标。
正切可以理解为y坐标与x坐标的比值。
三角函数在描述周期性和波动现象,如声波、光波等方面扮演着重要角色。这一特性使得它们成为分析这些现象的强大工具。
圆和圆周率(π):三角函数与圆密切相关,尤其在考虑角度和周期性时。
周期性和振动:这些函数在描述周期性行为,如振动和波动时,发挥着关键作用。
复数和欧拉公式:三角函数与复数紧密相关,特别是通过欧拉公式。这个公式可以描述为:“e 的 i*x 次方等于余弦 x 加上 i 乘以正弦 x”,其中,e 是自然对数的底数,i 是虚数单位。
傅里叶分析:三角函数用于信号处理和音频工程中的傅里叶分析,它们可以将信号分解为一系列的正弦和余弦波。
三角函数的周期性特点与圆的完美闭合形态紧密相连。绕圆旋转时,坐标在x轴和y轴上的投影(即余弦和正弦值)会周期性变化。
在直角三角形中,随着角度的变化,对边、邻边和斜边之间的比例也随之变化,形成了我们所熟悉的正弦、余弦和正切函数的波形。
单位圆上的每个点都通过余弦和正弦函数与特定角度相联系。这种联系不仅揭示了三角函数的几何基础,也展示了它们在更广泛的数学领域中的应用。
实际案例研究 - 三角函数在解决问题中的应用
三角函数不仅在理论上具有重要意义,它们在解决现实世界问题中也扮演着关键角色。这一部分将通过几个具体案例来展示三角函数的应用。
在建筑和工程设计中,三角函数用于计算斜面、坡度和结构的稳定性。例如,在建造桥梁时,工程师会使用三角函数来确保桥梁的斜拉索和支柱在各种负载下保持稳定。
在天文学中,三角函数用于计算星体的位置和轨道。通过测量角度和距离,天文学家能够精确地确定星体相对于地球的位置,这对于导航和深空探测至关重要。
在物理学中,三角函数被用来描述和分析波动,如声波和光波。通过分析这些波的频率、振幅和相位(都与三角函数相关),物理学家可以更好地理解声音和光的传播机制。
地理信息系统中,三角函数用于计算地球表面的不同点之间的实际距离。这在规划道路、桥梁建设以及环境监测等领域都有着重要应用。
跨学科联系 - 三角函数与其他学科的关系
三角函数的应用远远超越了纯数学领域,它们在其他学科中也有着深远的影响。
在代数和解析几何中,三角函数用于表示和解析各种几何形状和运动。例如,在解析几何中,三角函数帮助数学家和工程师理解和计算曲线的特性,如螺旋线和波浪形状。
在物理学领域,三角函数是理解和计算力学、波动学和电磁学问题的基础。它们用于计算物体在力的作用下的运动轨迹、波的传播以及电磁场的分布。
在工程学中,三角函数不仅用于设计和构建结构,还用于解决诸如力的分析、物质的流动和能量的传输等问题。例如,在电气工程中,交流电路的分析便广泛应用了正弦和余弦函数。
在计算机科学中,三角函数用于计算机图形学和数字图像处理。它们帮助计算机程序模拟真实世界的视觉效果,如光线的折射和物体的旋转。
三角函数的现代应用
三角函数在现代科学和技术中的应用同样广泛且关键,特别是在新兴技术和科学研究领域。
在计算机图形学中,三角函数是创建逼真图像和动画的基础。通过使用正弦和余弦函数,计算机程序能够模拟光影效果、物体运动和视角变换,这在视频游戏设计、电影特效以及虚拟现实技术中至关重要。
在电子工程和通信领域,三角函数在信号处理中扮演着核心角色。它们用于分析和合成信号,特别是在处理音频和视频数据时。通过傅里叶变换,复杂的信号可以分解为一系列简单的正弦和余弦波,这对于数据压缩、噪声过滤和信号恢复等应用至关重要。
在量子物理学领域,三角函数帮助科学家描述和预测微观粒子的行为。它们在量子力学的波函数、概率幅和干涉模式中发挥着关键作用。
在机器人学和自动控制系统中,三角函数用于编程和控制机器人的运动。例如,在设计机械臂时,工程师使用三角函数来计算关节角度和位置,以确保精准的运动控制。
结论:三角函数的综合视角
通过对三角函数的探索,我们不仅了解了它们在几何和代数中的根基,还发现了它们在现代科学和技术中的广泛应用。三角函数不仅是数学中的一个重要分支,更是连接不同学科和实际应用的桥梁。
数学与现实世界的链接:三角函数展示了如何将纯粹的数学理论应用于解决实际问题。从古代建筑师的计算到现代科技的突破,三角函数一直是创新和发现的基石。
跨学科的重要性:三角函数在物理学、工程学、计算机科学等众多领域中的应用,凸显了数学在跨学科研究中的核心作用。它们不仅解决具体问题,还促进了不同学科之间的融合和交流。
未来的探索:随着科技的发展,三角函数在新兴领域的应用仍有巨大潜力。无论是在深海探测、宇宙旅行还是量子计算领域,三角函数都可能成为推动未来发展的关键。