高等数学的核心内容——微积分

【思政目标】“坚持真理、勇于探索、求实创新”的思政目标
微积分是基于极限而创建的,是高等数学课程教学中的核心点所在。现代微积分体系的形成,要归功于众多科学家的共同努力。微积分研究的是微分与积分的矛盾,微积分基本定理时揭示微分与积分的既对立又统一的规律。人类由极限的原始思想到柯西、魏尔斯特拉斯的ε-δ的极限形式化严格定义,牛顿-莱布尼兹的流数术到现代微积分体系的建立无不闪耀着数学的创新精神。数学是人类经历上万年的漫长探索与研究逐渐积累而成的,一代又一代的数学家为此付出了艰辛的能力,同时也逐渐形成了他们的集体人格:对理性思维的坚信与传承、尊重事实、坚持真理、实事求是、勇于怀疑、勇于批判、勇于探索、坚持不懈、敢于创新就是数学家集体人格的主要表现。
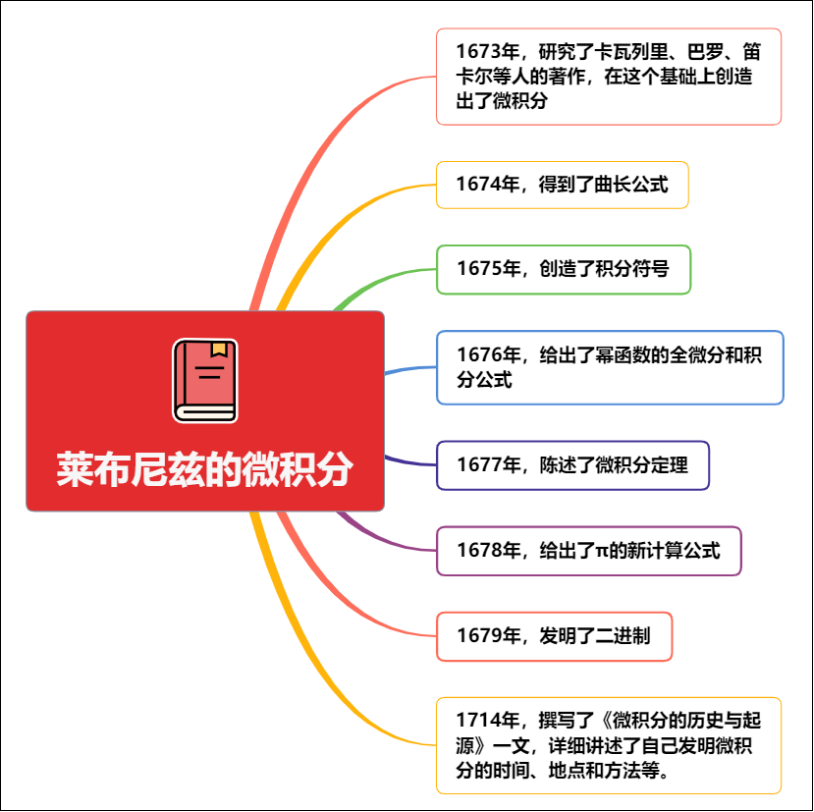
例如,微积分学开创人德国科学家莱布尼兹,他是先成为哲学家,而后成为数学家的,现在我们所学微积分定理和符号等重点知识很多也是莱布尼兹给出的,法国数学家笛卡尔首先也是一位哲学家。马克思与恩格斯,在学生眼里都是文科生,但这两位先哲在微积分领域均有很大成就,其见解独特,并从微积分知识中不断汲取养分,马克思自从牛顿和莱布尼兹创始了纯数学的里程碑微积分之后,很感兴趣,专门研究微积分,为此马克思为研究微积分手稿1000多页,很多结论非常重要。通过研究,也让马克思获取了揭示人类发展规律的灵感源泉和思想动力。
爱国情怀:通过介绍我国在高铁、航天等领域的科技进步,激发学生的爱国情怀和民族自豪感,引导学生树立科技报国的理想。
科学精神:通过讲述微积分的发展历程和著名数学家的故事,培养学生的科学精神和探索精神,鼓励学生敢于质疑、不唯权威、勇于探索未知领域。
工匠精神:在导数与微分的计算和应用中,注重培养学生的严谨细致、精益求精的工匠精神,让学生在数学学习中体验到精益求精的乐趣和成就感。
辩证唯物主义思想:通过导数与微分的学习,引导学生用发展的眼光看待事物,理解事物之间的内在联系和变化规律,树立辩证唯物主义的世界观和方法论。
导数与微分(学时数:10学时)
1.课程主要内容
导数的概念,函数的求导法则,高阶导数,隐函数和由参数方程所确定的函数的导数,函数的微分。
2.重点和难点
【重点】导数、微分的概念,导数的运算,微分的一阶形式不变性。
【难点】复合函数的求导法,隐函数和参数式所确定的函数的导数。
导数与微分是微积分的重要组成部分,导数是解决函数的变化率问题,微分是解决函数的改变量问题。微分概念的建立依赖于导数概念,而导数又是函数的微分与自变量微分的商,求导数与求微分的方法基本上是一致的,因此导数是重点。通过完成本章达标实训练习,可使读者达到以下要求。
一级达标要求:准确理解掌握导数与微分的概念及其几何意义,能够熟练掌握导数基本公式及求导法则,包括函数的和、差、积、商与反函数、复合函数求导并熟记基本初等函数与常见的初等函数的导数表达式。掌握微分运算法则、微分形式的不变性,会求函数的微分。
二级达标要求:在一级达标要求的基础上,理解连续、可导、可微、连续可导之间的关系,能够掌握隐函数、参数方程所确定的函数及抽象函数的求导法,理解高阶导数的概念,掌握求初等函数高阶导数的方法,能解决关于导数与微分的综合应用问题。
【数一】导数和微分
考试内容
导数和微分的概念,导数的几何意义和物理意义,函数的可导性与连续性之间的关系,平面曲线的切线和法线,导数和微分的四则运算,基本初等函数的导数复合函数、反函数、隐函数以及参数方程所确定的函数的微分法高阶导数一阶微分形式的不变性。
考试要求
1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.
2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.
3.了解高阶导数的概念,会求简单函数的高阶导数.
4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.
【数二】导数和微分
考试内容
导数和微分的概念、导数的几何意义和物理意义、函数的可导性与连续性之间的关系、平面曲线的切线和法线、导数和微分的四则运算、基本初等函数的导数、复合函数、反函数、隐函数以及参数方程所确定的函数的微分法、高阶导数、一阶微分形式的不变性。
考试要求
1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.
2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.
3.了解高阶导数的概念,会求简单函数的高阶导数.
4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.





