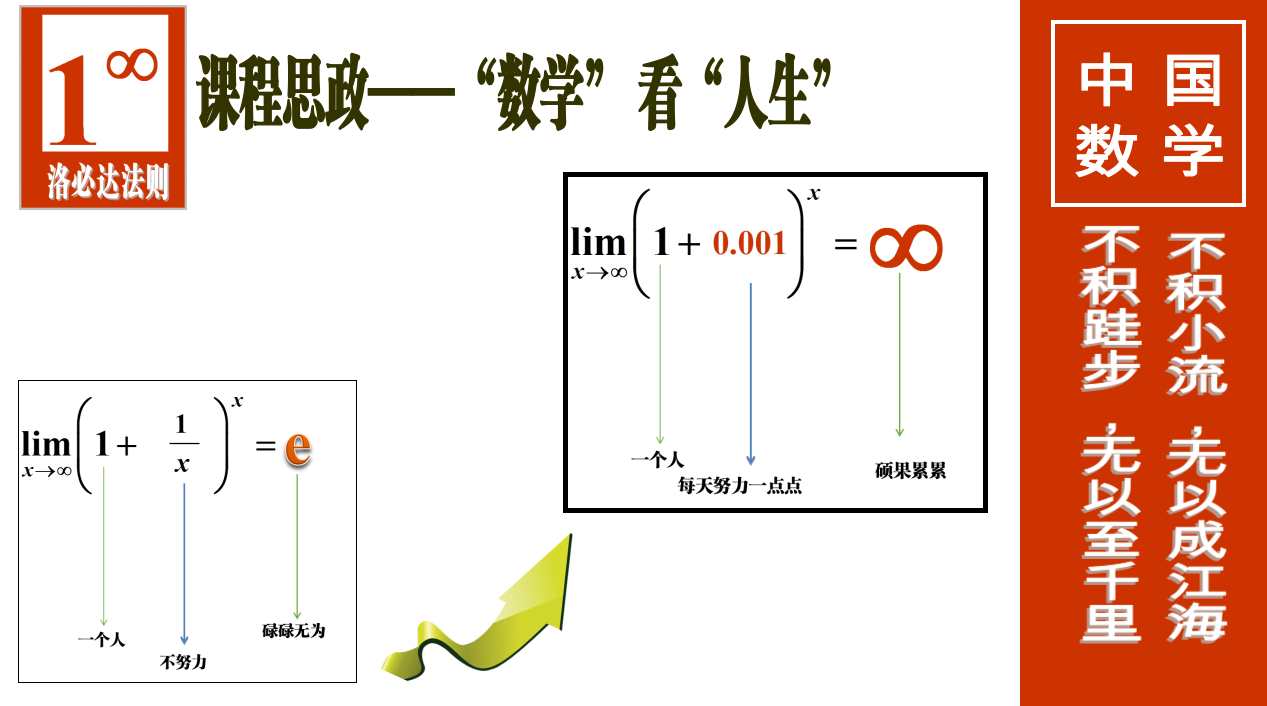
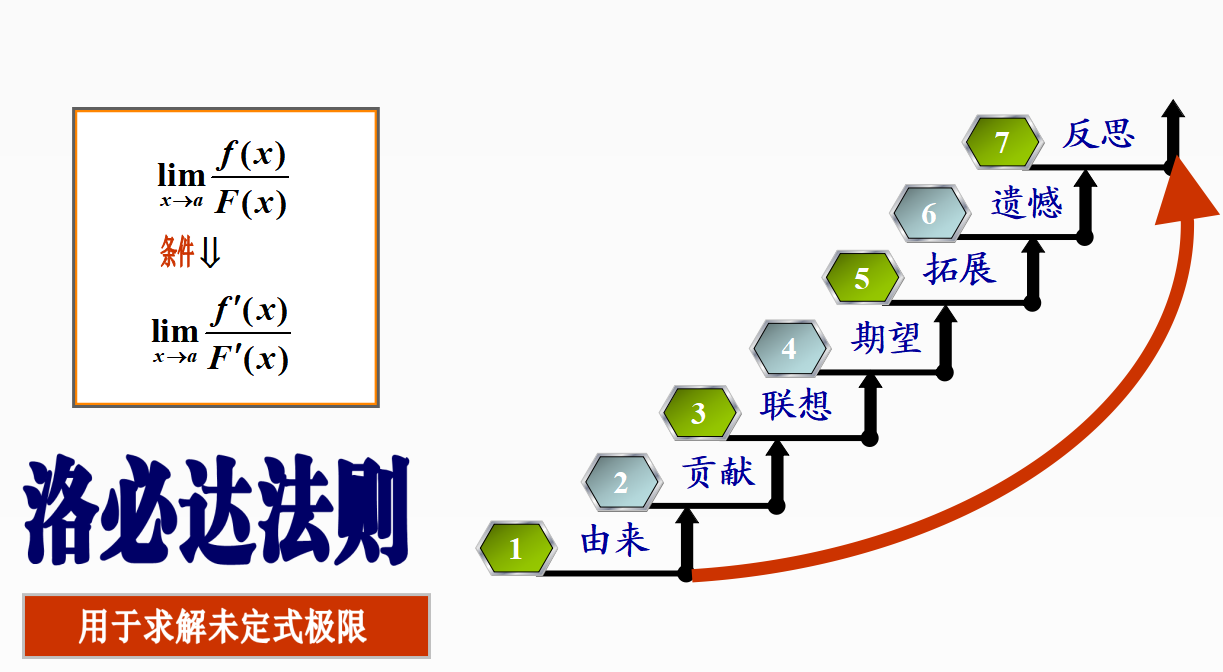
洛必达法则作为数学中的一个重要定理,不仅在数学领域有着广泛的应用,还蕴含着丰富的数学文化。
一、历史背景
洛必达法则是由法国数学家洛必达(L’Hôpital)在18世纪提出的,这一法则的提出极大地推动了微积分学的发展,为求解复杂极限问题提供了有力的工具。洛必达法则的提出,不仅体现了当时数学家们对微积分学深入研究的成果,也反映了他们对数学严谨性和实用性的追求。

二、数学意义
洛必达法则是微分学中的一个重要定理,主要用于求解“0/0”或“∞/∞”形式的未定型极限。这一法则的基本思想是通过求导来简化极限计算,将复杂的极限问题转化为更容易求解的形式。洛必达法则的应用不仅限于简单的分数形式极限,还可以扩展到更复杂的函数极限问题中,如复合函数、三角函数、指数函数和对数函数的极限等。
三、文化价值
促进数学发展:洛必达法则的提出和应用,推动了微积分学的发展,为后来的数学研究提供了重要的理论基础。同时,它也激发了数学家们对更复杂数学问题的探索和研究。
培养严谨精神:洛必达法则的使用需要严格的条件限制和精细的运算过程,这要求数学家们具备严谨的数学思维和细致入微的运算能力。这种严谨精神是数学文化的重要组成部分,对于培养数学人才具有重要意义。
展现数学之美:洛必达法则通过将复杂的极限问题转化为简单的导数问题,展现了数学中的简洁美和对称美。这种美不仅体现在数学公式的形式上,更体现在数学思想的深度和广度上。
四、学习心得
洛必达法则在数学教育中具有重要的地位。它不仅是高等数学课程中的重要内容,也是提升数学思维和解题能力的重要手段。通过学习洛必达法则,同学们可以掌握求解复杂极限问题的方法,提高数学运算能力和逻辑思维能力。
综上所述,洛必达法则作为数学文化的重要组成部分,不仅具有深远的历史背景和重要的数学意义,还蕴含着丰富的文化价值和教育意义。它不仅是数学家们智慧的结晶,也是人类文化宝库中的瑰宝。