第一节 平面任意力系向一点的简化
上一节
下一节
平面任意力系:各力的作用线在同一平面内,既不汇交为一点又不相互平行的力系,叫平面任意力系。
根据力的平移定理,将平面一般力系等效变换为作用于其平面内任一点O的平面汇交力系和平面力偶系,这就是平面一般力系向任一点O的简化方法。点 O称为简化中心。
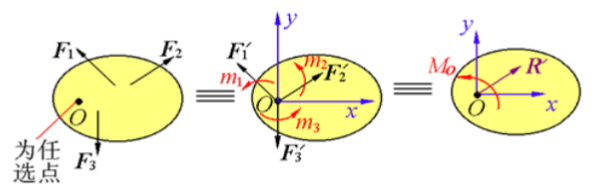
这样,就进行了平面任意力系向作用面内任一点 O的简化。即:平面任意力系向作用面内任一点 O简化,得到一个合力 R' 和一个合力偶 Mo。 合力R'称为原力系的主矢,等于原力系各力的矢量和;合力偶 Mo称为原力系对简化中心O的主矩,它等于原力系中各力对简化中心O的矩的代数和。
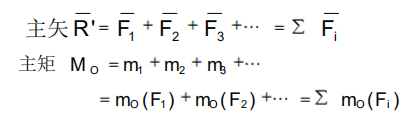
应该注意:力系的主矢与简化中心的位置无关; 而主矩一般情况下与简化中心的位置有关,因此对主矩必须标明简化中心。
上面讨论的是平面任意力系向作用面内任一点简化的一般情况,还有一些特殊情况:
( 1) 若 =0 , M o ≠0,即简化结果为一合力偶M o = M ,此时刚体等效于只有一个力偶的作用, 因为力偶可以在刚体平面内任意移动,故这时主矩与简化中心 O无关。
(2)若 ≠0,M o =0,即简化为一个作用于简化中心的合力。这时简化结果就是合力(这个力系的合力),
=
(此时与简化中心有关,换个简化中心,主矩不为零)
(3)若 ≠0,Mo ≠0,为最一般的情况。此种情况还可以继续简化为一个合力
。合力
的大小等于原力系的主矢, 合力
的作用线位置d=
。
(4)若 =0, Mo=0,则力系处于平衡状态。


