第一节 力矩、力偶和力偶矩
上一节
下一节
一、力矩
力除了能使物体移动外,还能使物体绕某一点转动。把力的大小与力臂的乘积称为力矩,用 MO (F)表示,即
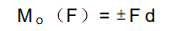
式中,点 O称为力矩中心,简称矩心。矩心 O到 F 的作用线的垂直距离 d称为力臂,力矩的单位为 N·m。正负符号表示力矩的转向。
一般规定 :力使物体作逆时针转动的力矩为正,反之为负。
二、合力矩
平面汇交力系的合力对平面内任一的力矩,等于力系中各分力对同一点的力矩的代数和,这就是合力矩定理。即
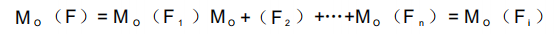
三、力偶
1. 力偶的概念
对物体施加一对大小相等、方向相反、作用线平行但不在同一条直线上的两个力,使物体产生纯转动,称这对力为力偶。
力偶中两个力之间的垂直距离 d 称为力偶臂。
2. 力偶的特性
(1)力偶是大小相等、方向相反、作用线平行的两个力,没有合力;
力偶在任何坐标轴的投影的代数和等于零。
(2)力偶不能与一个力平衡,必须用力偶来平衡。
(3)大小、作用面、转向三要素相同的力偶都是等效力偶。3
(4)力偶与力矩的共同点是能改变物体的转动状态,不同点是力矩使
物体的转动效应与矩心有关,而力偶对作用面内任何一点的矩为一常数。
3. 力偶矩
力偶对物体产生的转动效果取决于这两个力的大小和两个力之间的垂直距离的乘积,称为力偶矩,用 m(F、F')表示,即
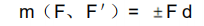
式中, F——力的大小(N·m);d——力偶臂。
注意 :与力矩相似,力偶矩也有方向。一般规定:使物体作逆时针转动的力偶矩为正,反之为负。


