一、力系:同时作用在物体上的一组力。
二、等效力系:两个力系对物体的作用效应相同,则称这两个力系互为等效力系。当一个力 与一个力系等效时,则称该力为力系的合力;而该力系中的每一个力称为其合力的分力。把力系中的各个分力代换成合力的过程,称为力系的合成;反过来,把合力代换成若干分力的过程,称为力的分解。
三、平衡力系:若刚体在某力系作用下保持平衡。在平衡力系中,各力相互平衡,或者说,诸力对刚体产生的运动效应相互抵消。可见,平衡力系是对刚体作用效应等于零的力系。
四、合力和分力:若一个力和一个力系等效,则该力系称为合力,力系中各力称为此力的分力。
四、平面汇交力系 的合成方法
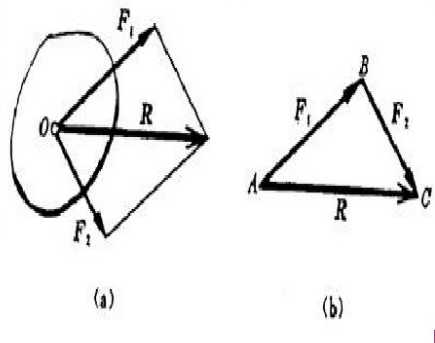
几何法:首先回顾用几何法合成两个汇交力。如图a,设在物体上作用有汇交于点的两个力F1和 F2,根据力的平行四边形法则,可知合力R的大小和方向是以两 力F1和F2为邻边的平行四边形的对角线来表示,合力R的作用点就是这两个力的汇交点。也可以取平行四边形的一半即利用力的三角形法则求合力如图b。
对于由多个力组成的平面汇交力系,可以连续应用力的三角形法则进行力的合成。设刚体上作用有一个平面 汇交力系F1、F2、…、Fn,各力汇交于A点(图1-1-2a)。根据力的可传性, 可将这些力沿其作用线移到A点,从而得到一个平面共点力系(图1-1-2b) 。 故平面汇交力系可简化为平面共点力系,连续应用力的平行四边形法则,可将平面共点力系合成为一个力。在(图1-1-2b)中,先合成力F1与F2 (图中未画出平行四边形),可得力FR1,即FR1 = F1+ F2;再将FR1与F3合成为力FR2,即FR2 = FR1+ F3;依此类推,最后可得:
FR=F1+F2+…+Fn=∑Fi
因此,平面汇交力系的合成结果是一个合力, 合力的作用线通过汇交点,其大小和方向由力系中各力的矢量和确定。需要指出的是,利用几何法对力系进行合成, 对于平面汇交力系,并不要求力系中各分力的作用点位于同一点,因为根据力的可传性原理,只 要它们的作用线汇交于同一点即可。


