《孙子算经》是我国古代的一部数学入门教材，其作者和成书年代都无定论. 书中有道题可谓“脍炙人口”，即“鸡兔同笼”问题：

今有雉（鸡）兔同笼，上有三十五头，下有九十四足。问雉、兔各几何？

对于学过代数的人来说，解此题自然是小菜一碟. 设鸡有 x 只，兔有 y 只，则相当于解线性方程组 I：

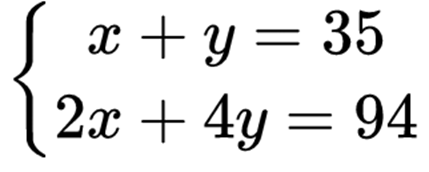
但《孙子算经》却用更简捷的算术方法来解：脚数的一半减头数，即 94/2-35=12 为兔数；头数减兔数即 35-12=23 为鸡数.

这是怎么想到的？可以这样解释：假设砍去每只鸡、兔一半的脚，则鸡成了“独脚鸡”，兔成了“双脚兔”；于是“独脚鸡”和“双脚兔”的总脚数就由 94 变成了 47；而每只“独脚鸡”的头数与脚数是相同的，每只“双脚兔”的头数比脚数少 1；故“独脚鸡”和“双脚兔”的总脚数与总头数之差，就是兔子数.

细细体会这个思路，你会发现它把注意力放在了头和脚的关系上. 设有 z 只兔子，砍掉一半兔脚，即 2z 只脚，则鸡和“兔”统一为“一头双脚”动物，不妨设其总头数为 w. 于是有线性方程组 II：

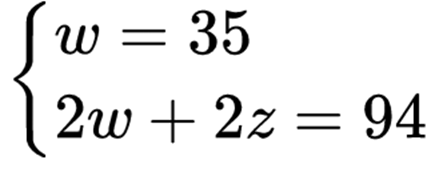
这个问题对我们有没有一点启示？面对现实中的问题，我们事实上可以从不同的角度出发，建立起不同的数学模型. 而不同的模型，其求解复杂度可能是不一样的. 比如同样的“鸡兔同笼”问题，我们从两种思路出发，得到了两个线性方程组. 但是这两个方程组都反映同一个原始问题，所以它们必定有密切联系，可以相互转化.

不难看到，线性方程组 I 可由线性方程组 II 经过“换元”得到，反之亦然：