《九章算术》是我国古典数学早期的一部名著，成就非凡，影响深远. 书分成九章，其第八章“方程”，按现代的术语来说，主要是介绍线性方程组（多元一次方程组）之解法.

问题今译：今有上等稻 3 捆、中等稻 2 捆、下等稻 1 捆，共出 39 斗米；有上等稻 2 捆、中等稻 3 捆、下等稻 1 捆，共出 34 斗米；有上等稻 1 捆、中等稻 2 捆、下等稻 3 捆，共出 26 斗米. 问上等稻、中等稻、下等稻每捆各能出几斗米？

我们用 x, y, z 分别代表每捆上等稻、中等稻、下等稻的出米数，则该问题相当于求解如下线性方程组.

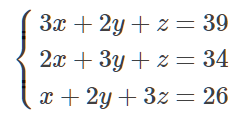
书中解法（术曰）：置上禾三秉，中禾二秉，下禾一秉，实三十九斗，于右方。中、左禾列如右方。以右行上禾遍乘中行，而以直除。又乘其次，亦以直除。然以中行中禾不尽者遍乘左行，而以直除。左方下禾不尽者，上为法，下为实。实即下禾之实。求中禾，以法乘中行下实，而除下禾之实。余如中禾秉数而一，即中禾之实。求上禾，亦以法乘右行下实，而除下禾、中禾之实。余如上禾秉数而一，即上禾之实。实皆如法，各得一斗。

解法今译：（我国古典数学的演算方式主要是“筹算”，就是把各种数量用算筹摆到台面上，然后按照一定的算法进行变换. 所以“术曰”前两句的现代意思是指列出如下数表.）

置上禾三秉，中禾二秉，下禾一秉，实三十九斗，于右方。中、左禾列如右方。

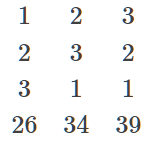
以右行上禾遍乘中行，而以直除。又乘其次，亦以直除。

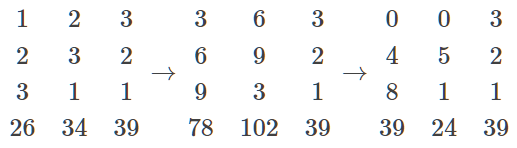
 然以中行中禾不尽者遍乘左行，而以直除。左方下禾不尽者，上为法，下为实。

实即下禾之实。（也就是说，已经解得 .）

求中禾，以法乘中行下实，而除下禾之实。余如中禾秉数而一，即中禾之实。

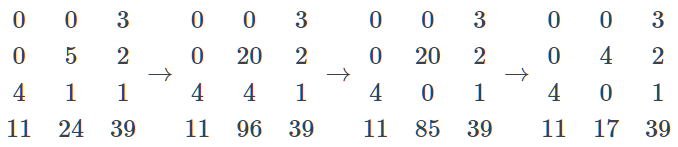
（此时已解得 .）

求上禾，亦以法乘右行下实，而除下禾、中禾之实。余如上禾秉数而一，即上禾之实。

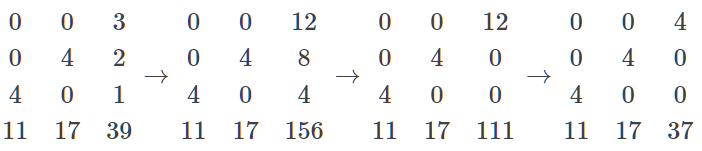
（这就得到了 .） 实皆如法，各得一斗。

以上例子已经体现了任意线性方程组的求解方法，一般被概括为“遍乘直除法”. 我们的祖先在两千年前就发现了这种方法，而西方直到十七世纪才明确提出类似算法，最终演变为我们即将学习的“高斯消元法”.

请阅读以下文章，了解消元法解线性方程组的发展史，思考该算法为何以高斯冠名.