课前学习任务
一个向量空间有很多基,而在欧氏空间中,可借助内积取出一种特殊的基,它具有非常优良的性质. 这种基就是所谓的正交基,由一组相互正交的向量组成. 欧氏空间一旦取定正交基,就相当于架起了我们中学所说的“直角坐标系”,于是各种计算推导就变得很方便了.
请认真观看视频,学习正交基的相关概念,了解它的优良性质,并完成以下测验.
课堂学习资料
课后学习任务
设  为欧氏空间 V 的一个基,通过 Gram-Schmidt 正交化得到标准正交基
为欧氏空间 V 的一个基,通过 Gram-Schmidt 正交化得到标准正交基 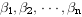 ,并设
,并设  到
到 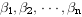 的过渡矩阵为 R.
的过渡矩阵为 R.
进一步,如果 V 是标准欧氏空间 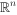 ,则有可逆矩阵
,则有可逆矩阵 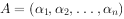 和正交矩阵
和正交矩阵 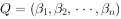 且
且 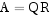 . 这是实际应用中很重要的一种矩阵处理方法—— QR 分解.
. 这是实际应用中很重要的一种矩阵处理方法—— QR 分解.
