课前学习任务

请认真观看视频，学习正定二次型的概念及判别法，并正确完成以下测验.

课堂学习资料

课后学习任务

我们在微分学中已经知道，要考察一个光滑函数在某一点附件的性态，可通过函数在该点处的 Taylor 展开式进行分析，因为它是对函数局部的近似. 就算把 Taylor 展开式的高次项全部舍弃，留下三次以下的项，也就是一个不超过二次的多项式，仍然能在足够小的局部范围内对函数达到较精确的近似.

例: 

利用 WolframAlpha 绘出函数图像如下：

可以看到函数整体上非常起伏，较为复杂. 如果我们关注它的局部，比如在 x=-1.57, y=0 附近，用 WolframAlpha 绘出函数图像如下：

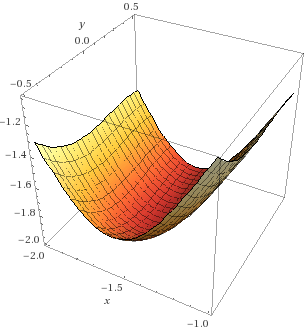
事实上利用 WolframAlpha 可知函数在 x=-1.5708, y=0 附近有一个驻点，再结合图像可知是极小值点. 我们在该点处将函数 Taylor 展开到二次项，得 ，即除了常数项 -2 外是一个正定二次型.

关于多元函数在某一点处的一阶、二阶“导数”及其在函数极值问题中的应用，请阅读资料：梯度与Hesse矩阵.